|
УДК 533.697.4
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОПТИМАЛЬНОГО ПОРЦИОННОГО ДОЗИРОВАНИЯ МАТЕРИАЛОВ
Московский государственный технологический университет "Станкин":
Сергей Николаевич Григорьев, ректор, проф., д.т.н.
Андрей Армович Грибков, зав. каф. "Металловедение", к.т.н.
В статье рассматривается задача математического описания процесса оптимального весового порционного дозирования. Для решения этой задачи определяются необходимые и достаточные параметры процесса дозирования. На примере поэтапного весового дозирования выявляются взаимосвязи выбранных параметров в случае оптимального дозирования и разрабатываются алгоритмы расчета оптимальных режимов дозирования.
In this article the author examined a problem of mathematical description of optimum weight batching. For decision of the problem the author determined necessary and sufficient batching process parameters. By example of stage-by-stage weight batching the author explored an interrelation of the optimum batching parameters and formulated optimum modes calculation algorithms.
Ключевые слова: математическая модель, порционное дозирование, оптимизация, режим, производительность.
Keywords: mathematical model, batching, optimization, mode, productivity.
Введение
Дозирование порошковых материалов играет важную роль во многих отраслях промышленности. В металлургической, химической, пищевой промышленностях качество и себестоимость производимой продукции напрямую зависят от точности дозирования и свойств используемых дозирующих систем. Производство конструкционных композитных материалов, инструментальных твердых сплавов, специальных пластмасс и других прогрессивных материалов, используемых в различных областях техники, в настоящее время не может быть реализовано без высокоточного порционного дозирования.
Автоматизация дозирования требует создания все более широкой номенклатуры автоматизированных систем дозирования порошковых материалов, повышения точности дозирования. Основой для создания новых, более эффективных по сравнению с существующими, автоматизированных систем дозирования является разработка математического описания процесса дозирования, включающего в себя выбор необходимых и достаточных параметров дозирования, характера их взаимосвязей, определение возможностей повышения точности и производительности дозирования.
Объем проведенных до настоящего времени теоретических исследований в области математического моделирования процесса дозирования весьма ограничен. Анализ мирового научного опыта свидетельствует, что фундаментальные исследования в данной области проводились главным образом в 1970-1980-х гг. на Украине и в России. К числу наиболее известных теоретических исследований относятся, в частности, работы Ю.В. Видинеева [1] и Е.Б. Карпина [2]. Однако Ю.В. Видинеев занимался в основном непрерывным дозированием, а Е.Б. Карпин - весовым неавтоматизированным оборудованием.
После достаточно длительного периода бездействия (продолжавшегося около 20 лет) в последние годы внимание к теоретическим исследованиям в области дозирования начало возрастать. В частности, было защищено несколько диссертаций в области структурного описания дозирующих систем и математического моделирования процесса дозирования [3, 4]. Также можно отметить интересное исследование по компьютерному моделированию процесса дозирования ("Оптимизация процесса весового дозирования сыпучих материалов"), проведенное в 2007 г. в Приднепровской государственной академии строительства и архитектуры (г. Днепропетровск, Украина). Условия для этого создали быстрое развитие вычислительной техники и появление профессионального математического программного обеспечения (в частности, программы MathLab, Maple и др.).
Однако ключевые задачи математического моделирования процесса дозирования до настоящего времени остаются нерешенными. В частности, не существует однозначного алгоритма для расчета режима порционного дозирования, т.е. функции интенсивности подачи материала от времени. Определению базовых подходов к решению указанной задачи посвящена данная статья.
Параметры математической модели дозирования
Описание процесса дозирования начинается с определения необходимого и достаточного комплекса параметров, характеризующих: во-первых, подачу материала (интенсивность и продолжительность), во-вторых, точность дозирующей системы (зависящей от точности элементов дозирующей системы и физико-механических свойств дозируемого материала), в-третьих, свойства дозируемой порции (величину порции и допустимую погрешность величины порции).
Параметры, характеризующие подачу материала и свойства получаемой порции, очевидны. В частности, если мы имеем дело с поэтапным дозированием, когда функция интенсивности подачи материала от времени является ступенчатой, в качестве параметров подачи материала выступают интенсивности подачи Q1, Q2…Qn (n - число этапов дозирования) и продолжительности дозирования T1, T2…Tn на этапах. Параметрами, характеризующими свойства дозируемой порции, являются масса порции M (в случае весового дозирования) или объем V порции (в случае объемного дозировании), а также максимально допустимая абсолютная Δ или относительная δ погрешность порции.
Для характеристики точности дозирующей системы (не следует путать ее с точностью дозирования!) необходимо ввести единую количественную характеристику. Это может быть сделано исходя из следующих соображений.
Основным источником случайной погрешности порционного дозирования является дисперсия количества материала, дозируемого за время отключения подачи материала. Это связано с непостоянством массы материала в столбе падающего дозируемого вещества и в колебании интенсивности подачи материала при отключении. В результате случайная погрешность порционного дозирования главным образом определяется интенсивностью подачи материала: чем выше интенсивность подачи, тем больше погрешность. Следовательно, искомая единая количественная характеристика погрешности дозирующей системы должна (в первом приближении) прямо пропорционально зависеть от интенсивности подачи материала. Поэтому искомая количественная характеристика погрешности дозирующей системы должна иметь размерность времени (произведение времени на интенсивность подачи дает массу). Назовем ее приведенной погрешностью времени дозирования K.
Физический смысл приведенной погрешности времени дозирования следующий: это время, за которое при заданной интенсивности подачи дозируется количество материала (масса или объем), равное абсолютной погрешности дозирования.
Математическая модель поэтапного дозирования
Математическая модель дозирования представляет собой совокупность функций, связывающих между собой все параметры дозирования. В данной статье мы рассмотрим математическую модель поэтапного весового дозирования.
Поэтапное дозирования является одним из наиболее эффективных типов дозирования [5-7]. При поэтапном дозировании процесс выдачи порции разбивается на этапы, причем на каждом последующем этапе дозируется меньшая часть порции с меньшей интенсивностью подачи материала. Погрешность дозирования на каждом из этапов (кроме последнего) компенсируется на последующем этапе, а погрешность дозирования на последнем этапе не должна превышать допустимую погрешность дозирования.
Используя ранее введенный параметр приведенной погрешности времени дозирования K, исходные зависимости для определения оптимального режима поэтапного весового дозирования определятся следующим образом:
Qi ×K(Qi, mi )=C×Qi+1 ×T i+1;
Qi=Δ/K(Qi, mi);
Q1 ×T 1 +Q2 ×T 2 +…+Qn ×Tn=M,
где K (Qi, mi ) ≈ K0 + kQi + hmi - приведенная погрешность времени дозирования, являющаяся в общем случае функцией от текущего значения интенсивности подачи Qi и накопленной массы порции mi ; K0, k, h - постоянные величины (коэффициенты); C - коэффициент запаса (рекомендуемое значение 3).
Поскольку величина приведенной погрешности времени дозирования изменяется в процессе дозирования незначительно (при правильной конструкции дозатора не более 5…10 %), мы приняли линейную зависимость величины K от интенсивности подачи и накопленной массы порции.
Математическая модель дозирования, очевидно, должна быть разработана применительно к оптимальному дозированию. Оптимальным будет такой режим, при котором обеспечивается удовлетворение одного из двух условий:
1. Режим дозирования обеспечивает максимальную производительность (минимальное суммарное время дозирования T ) при заданных свойствах материала и параметрах дозирующей системы.
2. Режим дозирования обеспечивает требуемую производительность (задаваемую через суммарное время дозирования T ) и точность (задаваемую через допустимую абсолютную погрешность D) дозирования заданной порции (в случае весового дозирования - массы M ) при минимальных требованиях к постоянству физико-механических свойств дозируемого материала и точности дозирующей системы.
В данной статье мы будем рассматривать первый случай оптимизации, который назовем оптимизацией по критерию производительности.
Проведем оптимизацию для двухэтапного дозирования по критерию производительности, т.е. определим параметры дозирования, при которых суммарное время дозирования минимально. Параметры двухэтапного дозирования связаны между собой следующим образом:
Q2=Δ/(K0 +kQ2 +hM) = 0,5(((K0+hM)2+4kΔ)0,5-K0-hM)/k;
T2=(CQ1(K0+kQ1 +h(M-T2Q2)))/Q2 =(CQ1(K0+kQ1 +hM))/(Q2(1+ChQ1));
T1=M / Q1 =(C(K0+kQ1 +hM))/(1+ChQ1).
Для нахождения оптимального режима продифференцируем функцию времени дозирования f = T1 + T2 по Q1 и приравняем полученное выражение к нулю
∂f/∂Q1=k/hQ2+(C2h2K0Q2–CkQ2h+C2h3MQ2+ChK0+Ch2M-k)/h(1+ChQ1)2Q2 - M/Q12=0;
откуда имеем уравнение четвертой степени относительно Q1:
khC2Q14 +2kCQ13+(C2hK0Q2 - CkQ2+CK0+ChM)Q12 - 2MhQ2CQ1 - MQ2 = 0.
Рассмотрим пример. Пусть M = 10 кг, Δ = 0,01 кг, K0 = 0,02 c, k = 0,005 с2/кг, h = 0,005 с/кг, число этапов n = 2. В результате расчета в соответствии с приведенными выше уравнениями получаем: Q1 = 2,3284 кг/с; Q2 = 0,1414 кг/с; T1 = 4,058 с; T2 = 3,896 с; TΣ = T1 + T2 = 7,954 с.
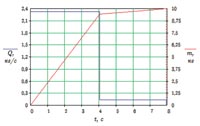На рис. 1 показан режим дозирования.
Рассмотрим теперь трехэтапное дозирование. Аналогичным образом для функции f = T1 + T2 + T3 находим минимум. При известном значении Q1 величина Q2 определяется (в соответствие с уравнениямм системы) следующим образом:
(khCQ1+kh2C2Q12+khCQ3)Q24+(2kQ1+2khCQ12-2kQ3)Q23+(MhQ1+Q1ChK0+Q1K0-khCQ12Q3- MhQ3+Q3K0+h2CMQ12- Q3h2C2MQ13)Q22 +(-2CQ13Q3hk – 2CQ12Q3hK0 – 2CQ12Q3h2M)Q2 – Q12Q3K0 – Q12Q3hM – Q13Q3k = 0.
Рассмотрим пример. Пусть условия будут такие же, что и в предыдущем примере, т.е. M = 10 кг, Δ = 0,01 кг, K0 = 0,02 c, k = 0,005 с2/кг, h = 0,005 с/кг, число этапов n = 3. В результате расчета в соответствии с вышеприведенными формулами получаем: Q1 = 5,4821 кг/с; Q2 = 0,9611 кг/с; Q3 = 0,1414 кг/с; T1 = 1,5182 с; T2 = 1,5234 с; T3 = 1,5034 с; TΣ = T1 + T2 + T3 = 4,5451 с.
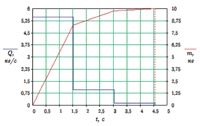На рис. 2 показан режим дозирования.
В данной статье мы не будем рассматривать математическое описание четырехэтапного дозирования. Это связано с чрезвычайно большим размером получаемых математических выражений. Проведенные исследования показали, что для определения оптимальных режимов в случае четырехэтапного дозирования, как и в случае трехэтапного дозирования, необходимо варьировать один из параметров, а остальные параметры определяются в результате решения уравнения четвертой степени.
Выбор численных методов для расчета оптимальных режимов
В случае двухэтапного дозирования расчет оптимального режима сводится к решению единственного уравнения четвертой степени, поэтому проблема выбора метода его решения не стоит. Любой из существующих методов решения уравнений (например, аналитическое решение Феррари) могут быть использованы.
В случае трехэтапного дозирования, когда осуществляется варьирование в достаточно широком диапазоне одного из параметров дозирования, и при каждом значении этого параметра необходимо решать уравнение четвертой степени, объем вычислений становится очень большим. Количество уравнений четвертой степени, которые необходимо решить в ходе одной оптимизации, достигает 250 тысяч. Кроме того, уравнения имеют сложные коэффициенты, каждый из которых требует нескольких сотен операций.
Принимая во внимание объем оптимизационных вычислений, принципиальным становится вопрос о производительности вычислений. Аналитическое решение уравнений четвертой степени вопреки ожиданиям оказывается недостаточно быстрым при 64-битном представлении вещественных чисел, обеспечивающим 15 значащих разрядов. Это обусловлено значительной погрешностью вычислений и необходимостью корректирования полученного результата с помощью итерационных методов.
Как показывает практика расчетов для случая трехэтапного и четырехэтапного дозирования, лучшую производительность при решении уравнений обеспечивает использование следующих двух методов.
Первый метод основан на совместном использовании метода "золотого сечения" (для начальной локализации корней), теоремы Штурма (для определения числа корней в выбранном диапазоне) и итерационных методов (для точного определения корня в малом диапазоне). Алгоритмы, реализующие метод "золотого сечения", формирования массива коэффициентов функций Штурма и итерационные алгоритмы достаточно быстродействующие. В результате объем оптимизационного расчета оказывается приемлемым. Для персонального компьютера (ПК) с тактовой частотой 2 ГГц и разрядностью 64 бит (прочие параметры ПК оказывают незначительное влияние) продолжительность (однопоточного) расчета для трехэтапного дозирования составляет около 40 с, для четырехэтапного дозирования - около 1,5 мин.
Намного более производительным является метод, основанный на преобразовании исходного уравнения в матрицу и определении ее собственных значений. Продолжительность оптимизационного (однопоточного) расчета с использованием данного метода составляет (при заданной выше мощности ПК) для трехэтапного дозирования около 2 с, а для четырехэтапного - около 5 с. При этом теоретически надежность данного метода немного ниже. Ошибки при использовании данного метода могут возникать, если у уравнения имеются нескольких близких по величине корней. На практике (составляющей на данный момент несколько тысяч различных оптимизационных расчетов) указанные ошибки пока не встречались.
Выводы
1. На базе ограниченного набора параметров потока материала, свойств получаемой порции и точности дозирующей системы возможна реализация адекватного математического описания и оптимизации режима поэтапного весового дозирования;
2. Практическая реализация оптимизации режима дозирования крайне трудоемка, однако может быть выполнена программными средствами;
3. Практические исследования скорости вычисления оптимальных режимов показали эффективность использования численных методов. В частности, для решения алгебраических уравнений высокого порядка целесообразно использовать метод собственных значений.
Литература
1. Видинеев Ю.Д. Дозаторы непрерывного действия. - М.: Энергия, 1978. - 184 с.
2. Карпин Е.Б. Средства автоматизации для измерения и дозирования массы. Расчет и конструирование. - М.: Машиностроение, 1971. - 469 с.
3. Давиденко П.Н. Исследование и разработка методов проектирования информационных систем на основе дозаторов дискретного действия: диссертация на соискание ученой степени кандидата технических наук. - Таганрог, 2005. - 192 с.
4. Колбасин А.М. Автоматизация технологического процесса управления производством многокомпонентных сыпучих бетонных смесей с учетом ошибок дозирования: диссертация на соискание ученой степени кандидата технических наук. - М., 2007. - 151 с.
5. Грибков А.А. Повышение точности и производительности автоматизированных систем весового порционного дозирования материалов //"Мехатроника, Автоматизация, Управление". - 2010. - №9. - C. 61-65.
6. Григорьев С.Н., Грибков А.А. Определение общих требований к точности элементов дозирующей системы // Технология машиностроения. - 2010. - №3. - C. 3-5.
7. Григорьев С.Н., Грибков А.А. Обобщенная оценка точности элементов дозирующей системы // Вестник машиностроения. - 2010. - №8. - C. 41-42.
Связь с авторами: andarmo@yandex.ru