УДК 621.458.034.022.5

ВИХРЕВАЯ МЕХАНИКА ВЗАИМОДЕЙСТВУЮЩИХ И ПЕРЕМЕЖАЮЩИХСЯ СРЕД В ПРОЦЕССАХ СМЕШЕНИЯ И ГОРЕНИЯ В КАМЕРАХ ДОЖИГАНИЯ РАКЕТНО-ПРЯМОТОЧНЫХ ДВИГАТЕЛЕЙ НА ТВЕРДОМ ТОПЛИВЕ

 Александр Григорьевич Прудников, начальник сектора ЦИАМ, д.т.н.
Артем Михайлович Подвальный, аспирант МГУПИ

 

Приводятся физические модели смешения, горения [1, 2] и перекрестного взаимодействия газогенераторных струй с воздушными струями в камере дожигания ракетно-прямоточного двигателя на твердом топливе и примеры решений замкнутой системы уравнений вихревой механики перемежающихся сред, для математических ожиданий геометрических и теплогазоаэродинамических параметров камеры дожигания ракетно-прямоточного двигателя на твердом топливе.

Their describes the physical model of mixing, combustion and gas jet cross-interaction with air jets in the afterburning rocket-ramjet chamber with solid fuel and examples of solutions of the closed system of equations of vortex mechanics alternating environments, for the math expectations of geometrical and thermogasаerodynamical parameters afterburning rocket-ramjet chamber with solid fuel.

Ключевые слова: ракетно-прямоточный двигатель, твердое топливо, камера дожигания, вихревая механика перемежающихся сред, вихревой слой, крупный вихрь, ядро потока.

Keywords: rocket-ramjet, solid fuel, afterburning chamber, vortex mechanics alternating environments, probability of occurrence, vortex layer, large vortex, core flow.

Опыт разработки воздушно-реактивной техники, начавшийся с 30-х годов [3], внес свои дополнения в декартово-эйлерову основу механики сплошных сред (МСС) [4]. Обычная скоростная фотография современного импульсного старта [1] перспективного беспилотного авиакосмического летательного аппарата демонстрирует участие в его выхлопе около двух десятков самостоятельных механик разных сред первого ряда (каскада). Специальные структурные скоростные снимки Фреймута, Рошко и др. авторов (в том числе из альбома Ван-Дайка) струйных, следовых и других "сдвинутых" скоростных потоков [2] демонстрируют до четырех каскадов более крупных лагранжевых объемов вращающихся сред. Эти среды, огороженные от внешней воздушной (атмосферной) среды бесконечно тонкими поверхностями контактного разрыва (ПКР), рождаются, растут, живут и распадаются ("умирают"), превращаясь в "турбулентные пятна" для пассивных струй или в "микротурбулентные очаги горения" с первого до четвертого каскада для струи горючего, по законам, изучаемым механикой взаимодействующих и случайно перемежающихся сплошных сред [2].

Большой интерес к ракетно-прямоточным двигателям на твердом топливе (РПДТ) проявляется в связи с интеграцией, то есть совмещением, рабочих параметров и характеристик ракетного двигателя (РД) на стартовом (разгонном) режиме полета и прямоточного воздушно-реактивного двигателя (ПВРД) на маршевом режиме полета [5]. Известно, что ПВРД работают в диапазоне чисел Маха ~1,6…7 [6], поэтому для его разгона используются РД, которые обладают рядом преимуществ на стартовом режиме полета.

Работами в области исследований и создания ПВРД в Советском Союзе занимались с 30-х годов. Уже в 1939 г. прошла летные испытания ракета Р-3 конструкции ученика Ю.А. Победоносцева - И.А. Меркулова, которая подтвердила перспективность применения воздушно-реактивных двигателей (ВРД) в авиации и ракетной технике [7].

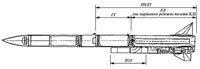В настоящее время основное внимание уделяется комбинированным схемам РПДТ (рис. 1) [6], обеспечивающим высокую полноту сгорания не только на стартовом режиме, но также на маршевом режиме полетах.

Для успешного решения основной задачи РПДТ надо иметь представления о физической природе смешения и горения струй горючего и окислителя в камере дожигания (КД) РПДТ.

В свою очередь, физические процессы смешения и горения очень сильно зависят от характера течения "сдвинутых" потоков (спутного воздушного и газогенераторного перекрестного). В данной работе рассматривается перекрестное взаимодействие потоков от газогенератора (ГГ-струй) с воздушными струями воздухозаборных устройств (ВЗУ).

Физическая модель данного расчета строится по вихревым моделям смешения и горения вихревой механики перемежающихся пассивных и реагирующих сред. Вихревая механика перемежающихся сред (ВМПС) - это механика, описывающая "пятнистую" структуру общего потока, состоящего из "разнородных" потоков (различных по цвету, плотности, составу и т.п.), участвующих в процессе смешения и горения (наш журнал достаточно подробно рассказывал об этой науке в нескольких статьях 2006-2008 гг. [2, 10] - Ред.).

К вихревым моделям смешения и горения ВМПС относятся следующие модели [8]:

-Модель постоянной завихренности (МПЗ) крупного вихря любого каскада, или вихря Ренкина, для любого сдвигового (вихревого) погранслоя (пристеночного, свободного, трубного, струи и следа). Данная модель вводит понятие ядра крупного вихря, внутри которого окружная скорость вихря растет по радиусу вихревого ядра линейно, а вне ядра (в надслое) - обратно пропорционально радиусу ядра вихря.

-Модель мгновенного захвата (ММЗ) (по аналогичной модели Сполдинга - engulfment) и модель вихревого клубка (МВК), или модель подпитки - entrainment, для двух разных фаз образования крупного вихря вихревого слоя из объемов двух спутных потоков. ММЗ предполагает мгновенное удвоение толщины сечения вихревого слоя, а МВК предполагает постепенное послойное увеличение с конечным тем же двойным увеличением начальной толщины вихревого слоя.

-Модель слияния - перинга (от англ. слова pairing - спаривание) двух крупных вихрей i-го каскада в крупный вихрь следующего (i+1) каскада. Данное явление для крупных вихрей подтверждено опытами Рошко (1976).

-Единая модель любого сдвигового слоя, состоящего из вихревого слоя, потенциального надслоя и потенциального (ламинарного) подслоя и т.п.

Определение средних параметров горящего вихревого слоя обеспечивают условно-осредненные по Рейнольдсу интегро-дифференциальные уравнения сохранения массы, импульса, энтальпии и уравнения вероятностей появления лагранжевых объемов крупных вихрей погранслоя каждой ГГ-струи, содержащих захваченные объемы трех взаимодействующих сплошных, но разных сред (горючие струи, воздушные струи, продукты горения).

Аналогичные уравнения существуют и для ядра воздушного потока, и для ГГ-струи, и для осесимметрично горящего основного вихревого слоя за конечным сечением ядра ГГ-струи. Сюда же входят решения такой же замкнутой системы, но для дисперсионных (пульсирующих) компонентов рассматриваемого случайного теплогазоаэродинамического (ТГАД) процесса; уравнения продольной компоненты импульса для перекрестного взаимодействия воздушных и горючих струй; соотношения условного статистического осреднения параметров каждой из трех упомянутых основных сред и четырех каскадов горящих крупных вихрей вихревых погранслоев, образующихся на границах перекрещивающихся воздушных и газогенераторных струй.

Всё это в краткой журнальной статье не имеем возможности привести.

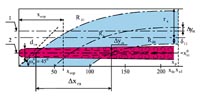При рассмотрении физических процессов смешения и горения уделялось внимание также и процессу перекрестного взаимодействия воздушных и горючих струй (см. схему взаимодействия ГГ-струи с воздушной струей на участке полного разворота xp, приведенной на рис. 2). В данной задаче разворота (при больших или малых углах наклона воздушной струи и соответственно при малых и больших диаметрах ГГ-струи) горючая струя может попасть либо в верхнюю левую часть зоны отрыва воздушного потока, либо в нижнюю правую часть зоны отрыва воздушного потока. В связи с этим появляется риск прожечь стенку КД из-за прилипания к ней факела пламени ГГ-струи в силу известного эффекта Коанда.

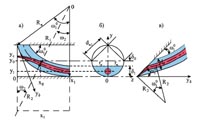Рассматривалась и схема определения оптимальных геометрических параметров разворота и соосности ГГ и воздушной струи после полного разворота. На рис. 3а, 3б показано оптимальное положение оси ГГ-струи в воздушном потоке, в котором в любой точке границы ГГ-струи должно присутствовать равное объемное содержание окислителя (воздуха), что безусловно сказывается на повышении полноты сгорания в КД РПДТ. На рис. 3в показано наилучшее расположение ГГ-струи в левом верхнем углу КД, что дает нам более раннее начало процесса смешения и горения, а в дальнейшем и полноту сгорания на более короткой длине КД. 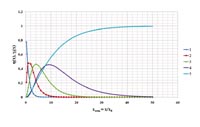На рис. 4 даны графики интенсивности и полноты дожигания.

С помощью методик, составленных по ВМПС, найдены параметры ГГ и воздушных струй свободного и принудительного разворота на входе в КД; определены координаты и необходимые параметры для соосности ГГ-струи и воздушной струи; геометрические размеры первой и второй зоны отрыва воздушных струй; длина ядра и длина факела пламени ГГ-струй; параметр спутности струй; параметр перегрева струй; скорость инжекции; положительный и отрицательный радиусы кривизны разворота ГГ-струй; полнота сгорания; концентрация горючего и температуры факелов пламени дожигания вдоль ГГ-струй; оптимальное расположение и углы входа ГГ и воздушных струй в КД [9].

Результатом исследований было аналитическое и графическое определение таких параметров и характеристик, как: x_яг - длина ядра ГГ-струи, F_1отр - максимальная площадь зоны отрыва воздушной струи, R_в - радиус принудительного разворота ядра воздушной струи, x_р - длина полного разворота ядра воздушной струи, η - полнота сгорания одиночного факела пламени диффузионного горения вдоль одной ГГ-струи. Они находятся соответствующими аналитическими решениями осесимметричных уравнений движения типа системы: x_яг/d⁰_гг = m⁰₁ × к_ν2 ( m⁰₁ -1)^-1;   F_1отр / F_{k = 1- q⁰1/ q11;}

R_в/d_k =(1- cosω⁰_в)^-1;  х_р/d_k=2π²r²_в1 r^-2_k sin²ω⁰₁×( sin²ω⁰₁ +2(l- cosω⁰₁))^-1; η=∫η_i (х)γ_i(x) dx,

где d⁰_гг- начальный изобарический диаметр ГГ-струи; m⁰₁ - начальный параметр спутности ГГ-струи; к_ν2 - среднее значение константы Толмина (для разных чисел Маха струи находится теоретически в рамках представлений ВМПС); F_К - площадь КД; q⁰₁, q₁₁ - газодинамические функции воздушного потока соответственно в начальном сечении и сечении полного разворота; d_k  - диаметр КД;  ω⁰_в - угол входа воздушной струи в КД; r_в1 - радиус входной части ВЗУ в КД; r_к - радиус КД; λ - относительная приведенная скорость воздушного потока с индексом соответствующего сечения.

В процессе работ были получены графики, соответствующие приведенным аналитическим соотношениям. Экспериментально (в трех характерных сечениях моделей КД [8, 9]) были подтверждены следующие данные: результаты расчетов по повышению полноты сгорания в КД РПДТ (с результатами в "холодном" экспериментальном исследовании смешения в модели КД); получено точное совпадение теоретически рассчитанного значения полноты сгорания (η = 0,75) с экспериментальным (η = 0,73) на определенной длине огневой КД модельного РПДТ; проведено сопоставление с полученными опытными данными аналитических решений радиусов разворота воздушных струй и необходимого для этого перепада давления.

Созданная на базе ВМПС методика по расчету теплогазоаэродинамических и геометрических параметров КД в условиях перекрестного взаимодействия воздушных и ГГ-струй показала: какое должно быть оптимальное размещение воздушных и ГГ-струй, количество и углы наклона сопел ГГ-струй на днище газогенератора, обеспечивающих максимальную полноту смешения и дожигания; какие должны быть положительные и отрицательные радиусы разворотов и конечные координаты осей всех струй, обеспечивающие высокую полноту дожигания и "холодные" стенки КД; целесообразность уменьшения длины КД за счет сокращения длины стартового заряда твердого топлива при одновременном увеличении его энергоемкости.

Литература

1. Прудников А.Г. Новый подход к теплогазоаэродинамическим процессам - силовой основе современных и перспективных авиакосмических, наземных и морских летательных аппаратов // Авиакосмическая техника и технология, № 1, 2008. - C. 40-50.
2. Прудников А.Г. Вихревая механика перемежающихся сред (пособие для всех интересующихся) // Двигатель, № 6, 2006; № 1, 2007; № 2, 2007.
3. Стечкин Б.С. Избранные труды: Теория тепловых двигателей. - М.: Физматлит, 2001. - 432 с.
4. Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. - 2-е изд., перераб. и доп. - М.: ГИТТЛ, 1953. - 788 с.
5. Ерохин Б.Т., Подвальный А.М. О взаимодействии рабочих процессов в диффузоре и камере смешения-сгорания РПВРД // В межвузовском сб. научных трудов. Информатика и технология. Материалы научно-практической конференции МГУПИ. Факультет ТИ. / Под ред. к.т.н., доц. Белова В.Г., д.т.н., проф. Крашенинникова А.И. - М.: МГУПИ, 2008. - С. 271-276.
6. Интегральные прямоточные воздушно-реактивные двигатели на твердых топливах (Основы теории и расчета) / В.Н. Александров, В.М. Быцкевич, В.К. Верхоломов и др. / Под ред. д.т.н., проф. Л.С. Яновского. - М.: ИКЦ "Академкнига", 2006. - 343 с.
7. Боев Д.А. Юбилей первого в СССР полета прямоточного воздушно-реактивного двигателя // Двигатель, № 3, 2009. - С. 32.
8. Podvalny A.M., Prudnikov A.G., Severinova V.V. Algorithms and methods for determining the geometrical, thermogasaerodynamical and structural parameters chamber afterburning rocket-ramjet with solid fuel [Электронный ресурс] // В сб. Авиадвигатели XXI века. Сборник тезисов III Международной научно-технической конференции. - М.: ЦИАМ, 2010. - С. 1094-1096. - 1 электрон. опт. диск (CD-ROM).
9. Подвальный А.М., Прудников А.Г. Методика расчета теплогазоаэродинамических параметров камер дожигания в условиях перекрестного взаимодействия воздушных и газогенераторных струй [Электронный ресурс] // В сб. Новые решения и технологии в газотурбостроении. Сборник тезисов докладов всероссийской научно-технической конференции молодых ученых и специалистов. - М.: ЦИАМ, 2010. - С. 154-155. - 1 электрон. опт. диск (CD-ROM).
10. Прудников А.Г., Боев Д.А. Модели и аналоги механики перемежающихся сред // Двигатель, № 1, 2007; № 2, 2007; № 2, 2008.
Связь с автором: 8 (903) 298-0061.