УДК 621.785.532

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ВАКУУМНОЙ ЦЕМЕНТАЦИИ УГЛЕРОДИСТЫХ И НИЗКОЛЕГИРОВАННЫХ СТАЛЕЙ

Михаил Юрьевич Семенов, главный инженер Академии
бюджета и казначейства Минфина России, к.т.н.
Людмила Петровна Фомина, начальник лаборатории
ФГУП "ММПП "Салют", к.т.н.

На основе экспериментального изучения формирования диффузионных слоев в ходе вакуумной цементации углеродистых и низколегированных сталей в ацетилене определены расчетные соотношения, описывающие массоперенос углерода в атмосферах низкого давления. Кинетические уравнения и граничные условия в параметрическом виде применены в математической модели процесса при циклических режимах науглероживания. Проведена проверка адекватности модели.

A computer simulation model of acetylene vacuum carburizing based on the kinetic equations of diffusion has been realized. This model of repetitive low pressure carburizing also include experimental values of coefficient of mass transfer and carbon potential. The calculated concentration curves are completely in accordance with results from laboratory experiments.

Ключевые слова: вакуумная цементация, математическая модель, диффузионный массоперенос, циклические режимы.

Keywords: acetylene vacuum carburizing, computer simulation model, diffusion mass transfer, repetitive heat-treatment.

Важным достоинством вакуумной цементации в ацетилене, диссоциирующем на поверхности стальной детали уже при температуре 900…960°С, является высокая равномерность насыщения [1]. Это обстоятельство, а также наличие вакуумных печей, оснащенных системой малодеформационной закалки, обеспечивающих стабильное высокое качество получаемых деталей, а также отвечающих требованиям по экологической безопасности и культуре производственного процесса, обусловливают широкое применение данного метода для упрочнения деталей машин, а также деталей ГТД [1, 2].

Вакуумную цементацию проводят в режиме циклической подачи ацетилена, при котором стадии насыщения чередуют с диффузионными стадиями, идущими при выключенной подаче газовой среды. Управляющим фактором процесса является временной режим циклической подачи ацетилена. Такой режим характеризуется достаточно большим числом вариантов циклических режимов. Экспериментальный перебор этих вариантов нецелесообразен по экономическим соображениям. В этой связи, наиболее эффективным способом подбора технологических факторов является применение математического моделирования.

Цель данной работы - обеспечение оптимального выбора технологических режимов вакуумной цементации на основе применения математического моделирования.

Вакуумную цементацию проводили на промышленной вакуумной установке в автоматизированном режиме. Исследования проводили на цилиндрических образцах Ж 25х15 мм, изготовленных из сталей 20 и 15Х. Насыщенность цементованного слоя определяли спектральным методом на оптико-эмиссионном анализаторе QSH-750 фирмы OBLF SPEKTROMETRIE GMBH. Объекты исследований перед химико-термической обработкой проходили предварительную термическую обработку.

При разработке модели вакуумной цементации использованы кинетические соотношения, апробированные в ранее предложенных математических моделях ионной цементации и высокотемпературной нитроцементации, описанных в работе [3].

Кинетическое уравнение диффузии углерода в аустените в одномерном представлении имеет классический вид.

В качестве выражения коэффициента диффузии углерода применяли классическое выражение Вэлса-Мелла [4] в форме:

D=Аexp{-BR^-1T^-1},                                                   (1)

где А=0,04+0,08С; В=131000; D=D(C, T) - коэффициент диффузии углерода в аустените, зависящий от концентрации углерода и температуры T; С=C(x, t) - концентрация углерода на глубине x от поверхности в момент времени t; R - универсальная газовая постоянная.

При моделировании диффузионных процессов в низколегированной стали 15Х влияние легирования на кинетику науглероживания учитывали путем введения дополнительного термодинамического коэффициента легирования, связывающих активности углерода в легированном и нелегированном аустените. Параметрические выражения термодинамических коэффициентов влияния легирования на термодинамическую активность углерода взяты из работы [5].

Вместе с тем принципиальное значение при разработке моделей диффузионного насыщения имеет определение граничных условий, отражающих происходящие на границе раздела металла и рабочей среды процессы. Наряду с обоснованностью выбора выражения коэффициента диффузии насыщающего элемента именно достоверность описания массопереноса углерода через поверхность раздела фаз, в основном, определяет адекватность всей математической модели.

Как показали проведенные эксперименты, в ходе активного насыщения стали высокая в начале процесса скорость массопереноса постепенно снижается, при этом поверхностная концентрация углерода стремится достичь своего максимума.

По мнению авторов, это обстоятельство обусловлено известной ограниченностью растворимости углерода в аустените. При этом в отсутствие значительного количества хрома и других сильных карбидообразующих элементов отсутствуют стимулы к активному росту избыточной карбидной фазы.

На диффузионной стадии при принудительном отключении массопереноса углерода из рабочей атмосферы происходит перераспределение углерода, перенесенного на стадии насыщения с поверхности вглубь металла.

Весьма существен тот факт, что в ходе проведения циклических процессов вакуумной цементации на диффузионных стадиях при отключение подачи технологических газов практически полностью отсутствует обратный отток углерода с поверхности металла в рабочую атмосферу, который имеет место при ХТО в обычных газовых средах.

Таким образом, на стадии насыщения в качестве граничного условия применяется выражение потока насыщающего элемента - углерода из технологической среды, то есть выражение первого закона Фика. Поток углерода пропорционален разности углеродного потенциала среды, то есть ее насыщающей способности при бесконечно большой продолжительности процесса, и концентрации углерода на поверхности, а также коэффициенту массопереноса, характеризующему скорость перехода атомов углерода из рабочей атмосферы в металл. Коэффициент массопереноса зависит от температуры процесса по аналогии с коэффициентом диффузии.

На диффузионной стадии граничное условие определяется наличием непроницаемой границы раздела фаз: науглероживающей среды и насыщаемого металла. Поэтому поток углерода на диффузионной стадии постоянно равен нулю. Таким образом, суммарное количество углерода в насыщаемом металле или интеграл от концентрационной кривой углерода по координате на диффузионной стадии остается постоянным. Это положение позволяет достаточно удобным образом находить частное решение дифференциального уравнения (диффузии), удовлетворяющее принятой физической модели на диффузионной стадии.

Учитывая изложенное, принятые положения физической модели процесса нашли свое отражение в граничных и начальных условиях, имеющих следующий вид:

в начальный момент времени на поверхности: C(x=0, t=0)=C0;

на стадии насыщения:

-D×С'(x=0)=J(t)= β_C(π_C-С(x=0));                                          (2)

на диффузионной стадии:

J(t)= 0 и определенный интеграл концентрации по всей глубине, равный суммарному количеству поступившего углерода: ∫Сdx= const,

где: С₀ - исходная концентрация углерода в стали; J = J(t) - изменяющийся в ходе процесса поток углерода через поверхность раздела фаз; β_C и π_C - значения углеродного потенциала и коэффициента массопереноса, соответственно, характеризующие свойства насыщающей атмосферы.

Значения β_C и π_C в настоящей работе определяли на основе кривых, полученных по результатам измерения содержания диффузионно-активного углерода на поверхности экспериментальных образцов, подвергнутых вакуумной цементации, в разные моменты времени процесса. Потенциалу pC соответствует концентрация углерода, достигнутая при достаточно длительном процессе насыщения. Значение β_C подбирали, исходя из кривизны кривых роста концентрации, при уже известном π_C.

Полученные параметрические выражения π_C и β_C подставили в соотношения (2).

Для расчета по предложенной математической модели, включающей в себя дифференциальное уравнение (одномерное уравнение диффузии), выражение коэффициента диффузии (1), граничные и начальные условия (2) (в параметрическом виде), применили явную разностную схему. Соотношения математической модели формализовали на языке программирования Object Pascal.

В целях проверки адекватности математической модели провели вакуумную цементацию образцов из сталей 20 и 15Х по циклическим вариантам режимов. Экспериментальные значения насыщенности образцов углеродом сравнили с полученными расчетным методом.

 

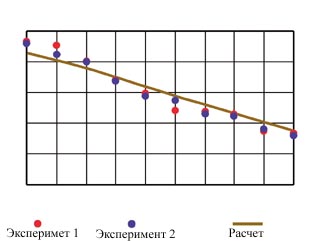
Рис. 1

На рис. 1 представлены экспериментальные значения и расчетная кривая значений концентрации углерода на образце из стали 15Х. Показано, что отклонение расчетных значений насыщенности углеродом от экспериментальных не превышает 0,1%. Аналогичные результаты получены и для стали 20. Таким образом, обеспечена удовлетворительная адекватность математической модели, достаточная для практического использования разработанного на ее основе программного средства для оптимального выбора вариантов технологических режимов для заданных характеристик диффузионного слоя.

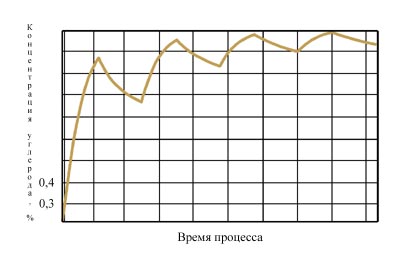
Пример рассчитанной кривой изменения концентрации углерода на поверхности в течение процесса представлен на рис. 2.

 

Рис. 2

Сложная динамика изменения поверхностной концентрации углерода, исходя из расчетной модели, объясняется тем, что движущей силой перераспределения концентрации на диффузионной стадии, в отсутствие отвода углерода из металла, является только градиент концентрации. При этом после первой стадии насыщения формируется наиболее крутопадающая концентрационная кривая. В дальнейшем кривые становятся все более плавными, градиент концентрации уменьшается и, следовательно, уменьшается движущая сила диффузионного выравнивания. Поэтому с каждым последующим циклом уменьшается значение разности поверхностной концентрации после стадии насыщения и концентрации после последующей диффузионной стадии.

 

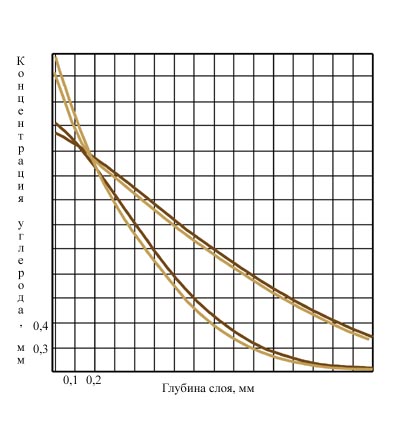
Рис. 3

Примеры расчета концентрационных кривых, соответствующих двум вариантам технологических режимов вакуумной цементации, представлены на рис. 3. Видно, как в результате проведения процессов науглероживания в атмосферах низкого давления по циклическим вариантам режимов цементации образуются плавные концентрационные кривые, характеризующиеся различной насыщенностью диффузионного слоя на поверхности (до значений концентрации углерода на поверхности 1,1…1,2%, рис. 3,а). При достаточной продолжительности процесса эффективная толщина слоя может достигать 1,5 мм (рис. 3,б) и даже более. Могут быть подобраны технологические режимы, при которых обеспечивается достаточно протяженная приповерхностная область высокой насыщенности углеродом (не ниже 90% от поверхностной концентрации), вплоть до 0,25 мм, что обеспечивает необходимый припуск на последующую после ХТО механическую обработку.

Таким образом, показаны широкие технологические возможности вакуумной цементации, реализация которых возможна на основе их оптимального выбора при помощи программного средства, основанного на разработанной математической модели.

Выводы

1. Определили на основе экспериментальных данных параметрические выражения углеродного потенциала и коэффициента массопереноса в ходе вакуумной цементации. Полученные параметрические выражения применили в математической модели вакуумной цементации в качестве граничного условия.

2. Установлена удовлетворительная адекватность разработанной математической модели при сравнении расчетных значений с экспериментальными результатами.

3. Показаны технологические возможности вакуумной цементации при оптимальном выборе технологических режимов расчетным методом.

Литература

1. Рыжов Н.М., Смирнов А.Е., Фахуртдинов Р.С. Особенности вакуумной цементации в ацетилене теплостойкой стали //МиТОМ, 2004. № 6. С. 10-15.
2. Производство зубчатых колес газотурбинных двигателей / Ю.С. Елисеев, В.В. Крымов, И.П. Нежурин и др. - М.: Высшая школа, 2001. - 493 с.
3. Семенов М.Ю. Разработка метода расчета режимов ионной нитроцементации, обеспечивающих заданный химический и фазовый состав диффузионного слоя легированных сталей: Автореф. дис. канд. техн. наук. - Москва, 1999.- 16 с.
4. Фромм Е, Гебхардт Е. Газы и углерод в металлах. Пер. с нем.- М.: Металлургия, 1980. - 712 с.
5. Могутнов Б.М., Томилин И.А., Шварцман Л.А. Термодинамика сплавов железа. - М.: Металлургия, 1984. - 206 с.

Связь с автором: fominalp@yandex.ru.