
|
УДК 669.293.782.018.44
ПЛОСКИЕ КОЛЕБАНИЯ ВРАЩАЮЩИХСЯ РОТОРОВ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ НА АНИЗОТРОПНО УПРУГИХ ОПОРАХ И ПРИ ОВАЛЬНЫХ КОЛЬЦАХ ПОДШИПНИКОВ
Юрий Борисович Назаренко, начальник бюро динамической
прочности ФГУП "ММПП "Салют", к.т.н.
Рассматриваются плоские колебания вращающихся роторов на анизотропных упругих опорах и при овальности колец подшипника. При вращении роторов на анизотропно упругих опорах и при овальности колец подшипника возникают гармонические нагрузки, которые действуют на вал и на диски роторов с частотой, равной удвоенной частоте вращения ротора, и возбуждают колебания роторов. На основе рассмотрения уравнений динамического равновесия вращающегося ротора на анизотропно упругих опорах и при овальности колец подшипника получено аналитическое решение и разработана методика определения критических частот вращения роторов, позволяющая простыми методами с применением метода конечных элементов (МКЭ) получать искомые результаты.
In this article the analysis of the planar vibrations of the rotating rotors on the anisotropic elastic support bearings and in case of the bearing ring out-of-roundness is presented. During the rotor rotation on the anisotropic elastic support bearings and in case of the bearing ring out-of-roundness the harmonic loads are brought about; these harmonic loads influence the shaft and the rotor discs with a frequency equal to a duplicated frequency of the rotor rotation and excite the rotor oscillations. The analysis of the equation of the dynamic balance of the rotating rotor on the anisotropic elastic support bearings and in case of the bearing ring out-of-roundness gave the opportunity to obtain the solution and to elaborate methods of estimating the value of critical revolution frequency of the rotors, which provide a means of calculation with a simple procedure using Finite element analysis (FEA).
Ключевые слова: ротор, вал, роликовый подшипник, межвальный подшипник, критическая частота вращения ротора, плоские колебания, собственная частота колебаний, анизотропно упругие опоры, овальное кольцо подшипника.
Keywords: rotor, bearing shaft, roller bearing, intershaft bearing, critical revolution frequency of the rotor, planar vibrations, self-resonant frequency, anisotropic elastic support bearings, bearing oval ring.
Введение
Динамические расчеты вращающихся роторов ограничиваются, как правило, рассмотрением регулярной прецессии. При синхронной прецессии изогнутая ось вала вращается с частотой вращения ротора и не совершает физических колебаний. Возникновение в этом случае физических колебаний ротора невозможно, так как центробежные силы будут этому препятствовать.
В работе [1, 2] рассматривалась возможность возникновения плоских колебаний при создании ударных нагрузок на опоре.
В данной работе рассматривается возможность возникновения плоских колебаний во вращающихся роторах на анизотропно упругих опорах и при овальном внешнем кольце подшипника. Это возможно при появлении в системе возмущающей силы, действующей синхронно с колебаниями.
Плоские колебания приводят к возникновению новой критической частоты, которая не определяется традиционными методами расчета [4].
Овальности колец подшипника могут иметь место как в процессе посадки подшипника с натягом так и образовываться в процессе эксплуатации из-за повышенных нагрузок при перегрузках, а также могут быть созданы специально для устранения проскальзывания тел качения слабонагруженных межвальных подшипников [3].
1. Кинематика движения ротора на анизотропно упругих опорах
Рассмотрим кинематику движения ротора на анизотропно упругой опоре и критику ротора по первой изгибной форме колебаний. Для оценки траектории движения ротора на анизотропной опоре "B" и влияния анизотропии на изгиб вала рассмотрим вал с одним диском (рис. 1).
При действии на диск (на расстоянии b от опоры В вала длиной L) центробежной силы FД при его дисбалансе на опоре В будет действовать сила равная FВ = FД·(L - b)/L. На изотропной опоре перемещения ротора составит RO = М·η·ω2(L - b)/СО·L, где М - масса диска; η - смещение центра масс диска относительно его оси вращения; ω - круговая частота вращения ротора; СО - жесткость изотропной опоры.
В случае анизотропных опор при различных жесткостях опор в направлении Х и Y ротор на опоре будет совершать эллиптическое движение (рис. 2).
Уравнение перемещения оси вала ротора в цилиндрических координатах на анизотропно упругой опоре от центробежной силы опишем тригонометрической функцией
R= RO + D·cos(2ωt), (1),
где D - амплитуда (максимальное значение) отклонения траектории вращения вала от круговой формы на опоре; t - время движения.
При отклонении траектории движения ротора от кругового движения на опоре будет возникать дополнительная реакция F = ΔF·cos(2ωt) и дополнительное линейное ускорение а = ΔF/m (где m - масса ротора, приходящаяся на анизотропную опору).
Амплитуду отклонения траектории вращения от круговой формы определим как перемещение от действия дополнительного ускорения при вращении ротора от т. А до т. В:
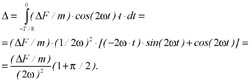 .
.
В то же время амплитуду отклонения контура от круговой формы можно определить из условия
RY = FB/CY и RX = FB/CX и она составит
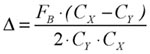 , (2)
, (2)
где СХ и СY - жесткости опоры в направлении осей Х и Y.
Подставляя (3) в (2), получим максимальное значение дополнительной силы, возникающей на анизотропно упругой опоре
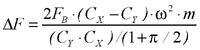 (3)
(3)
При этом при перемещении ротора от т. А до т. С на опоре будет действовать сила и ускорение, направленные в ту же сторону, что и прогиб вала.
Это ускорение приведет к уменьшению центробежной силы, вызывающей прогиб вала. Вал в этом случае будет уменьшать свой прогиб.
При перемещении ротора от т. С до т. D дополнительная сила на опоре будет действовать навстречу центробежной силе от неуравновешенной массы диска и в этом случае будет происходить увеличение прогиба вала.
Кроме этого дополнительная сила, возникающая из-за разности жесткостей в ортогональных направлениях, будет возбуждать вынужденные колебания ротора с удвоенной частотой его вращения.
Кинематика движения ротора на упругих опорах с овальным внешним кольцом подшипника
В случае овальности колец подшипника на опоре В ротор будет совершать эллиптическое движение (рис. 2).
Уравнение перемещения оси вала ротора в цилиндрических координатах на упругой опоре с овальным внешним кольцом от центробежной силы опишем тригонометрической функцией (1).
Ускорение, с которым вал на опоре будет перемещаться в радиальном направлении, определится как вторая производная по времени: а = -4Dω2·cos(2ωt).
При овальной траектории вращения ротора на опоре на диск будет действовать дополнительная сила
F= -ma·(L - b)/L.
Действие ускорения вала на опоре в одном направлении с его прогибом будет равносильно уменьшению действия центробежной силы, создающей его прогиб, и в противоположном направлении - увеличению.
Плоские колебания вращающегося ротора на анизотропных опорах и при овальном внешнем кольце подшипника
Для определения условия потери устойчивости ротора на критической частоте при возмущающей силе, действующей с удвоенной частотой вращения ротора, рассмотрим уравнения динамического равновесия инерционных и упругих сил вала одного диска при невращающемся роторе (рис. 3):
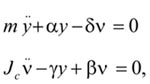 (4)
(4)
где α и γ - поперечная сила и момент от единичного прогиба вала в месте установки диска; δ и β - поперечная сила и момент от единичного углового смещения диска; m и JC - масса и осевой момент инерции диска; y и ν - поперечное перемещение и угол поворота диска.
Подставляя решение уравнений (4) в виде y = y0cos2рt и n = ν0·cos2рt, получим
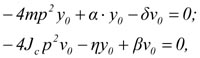 (5)
(5)
где y0 и n0 - амплитуда поперечных и угловых перемещений плоских колебаний; р - частота колебаний.
Для вращающегося диска в системе координат, связанной с ним (совершающей круговое движение с частотой ω), в уравнение (5) необходимо добавить центробежные силы и гироскопический момент.
Во вращающейся системе координат ротор совершает два движения: круговое вращение и гармоническое колебание.
Принимая для тонких дисков JC = Jp/2 и рассматривая прецессию как синхронную при изменяющихся значениях поперечных и угловых перемещений в соответствии с фазой колебаний, получим значение гироскопического момента
![]() (6)
(6)
где Jp - полярный момент инерции; λ - частота прецессии.
Подставляя решение уравнений в виде y = y0cos2ωt и n = n0·cos2ωt и после упрощений (6), получим уравнение плоских колебаний вращающегося ротора:
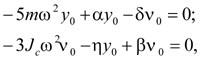 (7)
(7)
где у0 и n0 - амплитуды поперечных и угловых перемещений плоских колебаний вращающегося ротора.
Как видно из уравнений (7), при возбуждении колебаний дисков ротора силой, вызванной анизотропией опоры или овальностью колец подшипника, с удвоенной частотой его вращения, критическую частоту вращения ротора можно рассчитать как собственную частоту неподвижного ротора при увеличении осевого момента инерции дисков в три раза и увеличения их массы в пять раз.
Как видно из проведенных исследований, наличие анизотропии опор или овальности колец подшипников приводит к возникновению возбуждающей силы с удвоенной частотой вращения ротора, которая даже в отсутствии резонанса возбуждает вынужденные колебания ротора с удвоенной частотой его вращения.
Данное явление неоднократно наблюдалось и фиксировалось методами вибродиагностики в спектре частот на корпусах работающих двигателей.
Литература
1. Назаренко Ю.Б., Светашова Л.Ф. Проблемы надежности межроторного подшипника при динамическом взаимодействии роторов двухвальных турбореактивных двигателей//Двигатель. №3, 2010. - С.32-34.
2. Назаренко Ю.Б., Светашова Л.Ф. Критические частоты роторов газотурбинных двигателей при ударных нагрузках на опорах//Вестник двигателестроения. - Запорожье. - 2010. №2. - С.146-149.
3. Влияние овальности наружного кольца на долговечность высокоскоростного роликового подшипника /А.В.Швухов, А.Н. Пахомов Е.П. Жильников//Научно-технический конгресс по двигателестроению: сборник тезисов. - М., 2010. 150-152.
4. Хронин Д.В. Теория и расчет колебаний в двигателях летательных аппаратов. - М.: Машиностроение, 1970. - 411 с.
Связь с автором: nazarenkojb@rambler.ru