ВЗАИМОДЕЙСТВИЕ УДАРНЫХ ВОЛН

Олег Александрович Кирюханцев

Рассматривается задача взаимодействия ударных волн на поверхности полупространства в условиях стандартной атмосферы. Задача решается численно с использованием метода Годунова. Представлены результаты расчета давления в различные моменты времени.

Ударные волны играют важную роль в науке и технике и оказывают большое влияние на человека и общество. Под ударной волной обычно понимается крутой и тонкий фронт, возникающий при резком высвобождении энергии. Ударная волна движется подобно приливной волне и мгновенно повышает давление, плотность и температуру. В статье рассматривается процесс взаимодействия ударных волн, особенно актуальный при создании гиперзвуковых и детонационных двигателей.
Рассматривается система сходящихся ударных волн в условиях стандартной атмосферы. Требуется найти результирующие газодинамические параметры и характеристики течения.

Для моделирования рассматриваемых решений широко применяются различные численные методы: метод характеристик, методы типа Годунова, гибридные и другие схемы. Все они обладают теми или иными преимуществами и недостатками. В частности, метод характеристик трудно реализуется в трехмерном случае. В схемах типа сквозного счета разрывы "размазываются" на нескольких ячейках, что может дестабилизировать решение и даже привести к нарушению энтропийного условия. Под ним понимается уменьшение вычисляемого значения энтропии, что может привести к получению некорректного физического результата. Схемы типа Годунова являются монотонными, однако и для них (в случае высокого порядка) не доказана строгая энтропийность. Как следует из теории, в классах линейных схем высоких порядков монотонность не может быть достигнута. Однако схемы типа Годунова, не обеспечивая монотонности в строгом смысле, позволяют уменьшить амплитуду нефизических осцилляций.

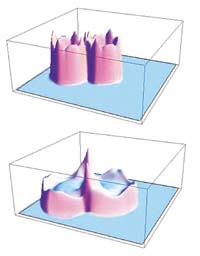Изменение давления в плоскости OXcYс полупространства в результате взаимодействия ударных волн в различные моменты времени

Для моделирования рассматриваемых процессов метод Годунова был дополнен элементами программной реализации, обеспечивающими решение нестационарных уравнений газовой динамики. Выбор определялся тремя основными обстоятельствами. Во-первых, схема сконструирована на основе физической сущности решаемой задачи - распада разрыва с образованием ударных волн, чего нельзя сказать об алгоритмах, формально аппроксимирующих дифференциальные уравнения дискретными аналогами безотносительно к физической сущности задачи. Выбранный метод автоматически обеспечивает выполнение законов сохранения. В других алгоритмах требуются специальные приемы и необходим контроль их выполнения. Во-вторых, важной особенностью метода является то, что он допускает расширение круга решаемых задач без кардинальной перестройки всего алгоритма. В-третьих, накопленный опыт применения метода Годунова свидетельствует о его высоком потенциале.

Параметры взаимодействующих воздушных ударных волн находятся путем решения известных уравнений газовой динамики [1].
Для построения схемы Годунова рассматриваемых уравнений применим метод конечных объемов. Для этого в системе координат {x_c, y_c, z_c} покроем всю вычислительную область Ω ячейками, т.е. разобьем ее на непересекающиеся, но граничащие друг с другом элементы объема так, чтобы каждый узел расчетной сетки содержался в одном элементе объема Ω_R = [0, I] [0, J] [0, K], где I, J, K - максимальные размеры расчетной области Ω в направлении осей x, y и z.

Результаты моделирования позволяют сформулировать следующие выводы:

- в зоне соударения волн наблюдается область повышенного давления и плотности, что согласуется с физикой процесса;
- в области соударения волн можно выявить сформировавшиеся области течения;
- для решения задач с требуемой точностью дополненный метод Годунова доказал свою эффективность.

Литература

1. Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных задач газовой динамики. - М.: Наука, 1976. 400 с.
2. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. - М.: Физматлит, 2001. 608 с.