ОПРЕДЕЛЕНИЕ КИНЕТИКИ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЛОПАТОК ТУРБИН С ИСПОЛЬЗОВАНИЕМ РАЗЛИЧНЫХ ВАРИАНТОВ УЧЕТА ПОЛЗУЧЕСТИ В ПРОГРАММНОМ КОМПЛЕКСЕ ANSYS

ФГУП "ЦИАМ им. П.И.Баранова": Борис Евгеньевич Васильев,
Любовь Александровна Магеррамова

Конечно-элементный комплекс ANSYS позволяет проводить расчеты, учитывая явление ползучести. Для лопатки турбины из жаропрочного никелевого сплава, работающей в течение длительного времени на одном режиме и подверженной действию неравномерного поля температур и центробежных сил, была определена кинетика НДС с использованием различных аналитических зависимостей.

При напряженно-деформированном состоянии (НДС) материала нелинейность изменения его свойств под действием нагрузки проявляется физически в виде "ползучести". В широком смысле это означает изменение во времени деформаций и напряжений, возникших при нагружении.

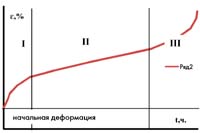Характерный вид кривой деформирования

В качестве источника информации о сопротивлении ползучести и длительному статическому разрушению (заключительному этапу деформирования материала) используются кривые ползучести, ε= f(t, σ, T) и кривые длительной прочности t_p = φ(σ , T), полученные на гладких цилиндрических образцах в условиях постоянной растягивающей нагрузки Р и температуры Т.

О сложности аналитического описания характеристик ползучести можно судить по классическому графическому изображению изменения деформации ползучести по времени, полученному по результатам испытаний в условиях постоянного напряжения и температуры.

Каждая группа материалов, характеризуемая общностью химического состава, технологией и структурным состоянием, должна обладать подобной реакцией на действие нагрузки и температуры, что в конечном виде отражается на форме экспериментальных кривых ползучести.

Для описания условий деформирования и разрушения сплавов при постоянных в процессе испытания нагрузке и температуре могут быть использованы аналитические или графические зависимости двух видов. Это либо уравнения, определяющие величину расчетных характеристик: деформации ( ε) или скорости ползучести (dε /dt) в зависимости от напряжений, времени и температуры, либо изохронные кривые.

В основе методики определения характеристик ползучести с помощью изохронных кривых лежит гипотеза о подобии кратковременной кривой деформирования в пластической области и кривых зависимости напряжений от деформации σ= f(ε ) в области ползучести при постоянных температурах (T = const).

Изохронные кривые сплава

Серия изохронных кривых отражает зависимость полной деформации от напряжения ε для нескольких значений времени (t = const для каждой кривой при заданной температуре). Расчет детали заменяется серией расчетов для каждого момента времени, для которого имеется изохронная кривая, которая используется вместо кривой мгновенного деформирования.

На множестве изохронных кривых - верхняя кривая - это диаграмма кратковременного деформирования, остальные, идущие ниже, отражают зависимость между напряжением и полной деформацией, включая деформацию ползучести для различных продолжительностей времени.

При расчете по изохронным кривым накапливающаяся деформация является пластической. Ввиду того, что эта методика относится к теории старения, она не может описать ступенчатое нагружение, так как согласно этой теории в момент изменения напряжения деформация ползучести должна иметь разрыв, что, очевидно, невозможно.
В качестве альтернативы этой методике в программном комплексе ANSYS можно использовать одно из предложенных уравнений, описывающих деформации и скорость ползучести на основании различных гипотез ползучести. Имеется возможность вводить и использовать другие зависимости.

Перед использованием какого-либо уравнения необходимо определять значения его коэффициентов, характеризующих применяемый материал. Следует отметить, что набор коэффициентов для всей области экспериментальных данных зависит не только от температуры, но и от уровня напряжений и длительности испытания. В связи с этим возникает необходимость проведения двумерной аппроксимации. Такая операция выполнима с помощью математического аппарата комплекса ANSYS.
Комплекс ANSYS в состоянии моделировать первые две стадии ползучести (первичную и вторичную). Третья стадия обычно не подвергается расчету, поскольку подразумевает приближение разрушения.

Указанный комплекс решает задачи ползучести, используя два метода интегрирования по времени. Оба метода применимы к расчетам статических или переходных процессов. Метод неявной ползучести является устойчивым, быстрым и точным; он рекомендован для общего использования. При выполнении расчетов можно использовать константы, зависящие от температуры, а также сочетать этот метод с моделью пластичности с изотропным упрочнением. Метод явной ползучести полезен в случаях, когда требуются весьма малые шаги по времени.

В программном комплексе ANSYS для прочностного анализа имеются 13 вариантов аналитических зависимостей, позволяющих определять величины деформаций и скоростей ползучести.

Для описания поведения лопаток из никелевого сплава из библиотеки ANSYS было выбрано несколько уравнений (метод неявного интегрирования).

Структуры уравнения для ползучести первой и для первой и второй стадий совместно представляют варианты записи известной гипотезы течения. Первое уравнение соответствует гипотезе упрочнения.

Для упрощения задачи определения коэффициентов уравнений может быть найден набор коэффициентов для различных постоянных температур. Коэффициенты, входящие в уравнения, были определены по результатам испытаний на ползучесть образцов из исследуемого материала.

Кривые ползучести, построенные с помощью полученных наборов коэффициентов уравнения, хорошо согласуются с экспериментальными кривыми при температуре испытания 1000 °С.

Время вычислений зависит от количества расчетных шагов. При использовании изохронных кривых необходимо заранее выбирать расчетные шаги по времени и их продолжительность. При использовании программного комплекса ANSYS количество шагов определяется программой. Важнейшим параметром является величина максимального относительного приращения деформации ползучести за один шаг по времени.

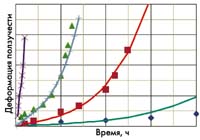Аппроксимация экспериментальных данных (точки)

Дополнительной трудностью является согласование коэффициентов для различных температур. Поскольку вычисление коэффициентов для промежуточных значений температур происходит с помощью линейной интерполяции, то при некотором их сочетании решение в ANSYS может привести к некорректным результатам. Например, значение деформации ползучести при промежуточной температуре при одинаковых напряжениях может "не лежать" между значениями деформации для крайних температур. Для получения более достоверных результатов необходимо, чтобы от температуры к температуре каждый коэффициент изменялся монотонно.

Анализ результатов показал, что при расчете на стационарном режиме выбор уравнения не играет принципиальной роли ввиду того, что коэффициенты уравнений подобраны для одних и тех же экспериментальных данных. Различие состоит лишь в удобстве подбора коэффициентов. Наиболее простым для аппроксимации экспериментальных данных и достаточно достоверным для решения задач определение кинетики напряженно-деформированного состояния лопаток из данного сплава является уравнение деформации ползучести. Что касается уравнений скоростей ползучести, то результаты, получающиеся при их использовании, менее достоверны, т.к. подбор коэффициентов осуществляется не для данных, полученных непосредственно из эксперимента, а для их дифференцированных значений.

Определение коэффициентов уравнения по гипотезе упрочнения сопряжено с наибольшими трудностями, что приводит к дополнительным ошибкам при выполнении расчетов.

Для решения задач вычисления кинетики напряженно-деформированного состояния и длительной статической прочности лопаток турбин при неизменной нагрузке рекомендуется использовать уравнение деформации ползучести с найденными по экспериментальным данным коэффициентами.

Литература

1. Каблов Е.Н., Голубовский Е.Р. Жаропрочность никелевых сплавов. М.: Машиностроение, 1998. С. 463
2. Малин Н.Н. Расчеты на ползучесть элементов машиностроительных конструкций (библиотека расчетчика). М.: Машиностроение, 1981. С. 221
3. Биргер И.А., Шорр Б.Ф. Термопрочность деталей машин. М.: Машиностроение, 1975. 455 с.
4. Басов К.А. ANSYS: справочник пользователя. М.: ДМК Пресс, 2005. 640 с.
5. Потапов С.Д. Численное моделирование и экспериментальное исследование напряженности вращающихся элементов турбокомпрессоров. Пенза: Информационно-издательский центр Пензенского гос. университета, 2002.

[Напоминаем, что Интернет-вариант статьи сильно сокращен. Ред.]