МЕТОДИКА ОПРЕДЕЛЕНИЯ НЕИЗМЕРЯЕМЫХ ПАРАМЕТРОВ ГТД ПО КОМПЛЕКСУ КОСВЕННЫХ ИЗМЕРЕНИЙ В ЭКСПЛУАТАЦИИ И СЕРИЙНОМ ПРОИЗВОДСТВЕ

Нина Сергеевна МЕЛЬНИКОВА, начальник отдела ФГУП "ММПП "Салют"

Представлена методика построения регрессионных моделей для определения основных параметров двигателя по комплексу косвенных измерений, приведен пример регрессионной зависимости для расчета температуры газа в камере сгорания.
В новых алгоритмах управления перспективными многофункциональными газотурбинными двигателями используются такие параметры двигателя, как, адиабатические к.п.д. узлов и другие параметры, измерение которых в настоящее время невозможно.

Автором разработана методика получения алгоритмов управления двигателем, основанная на использовании в реальном масштабе времени показаний штатных датчиков двигателя для вычисления на борту летательного аппарата основных эксплуатационных характеристик двигателя с помощью электронных цифровых регуляторов. Алгоритмы управления двигателем с использованием этой методики позволяют осуществлять оптимальное управление двигателем по выбранной функции цели с учетом изменения характеристик его узлов при серийном производстве и при выработке ресурса в процессе эксплуатации.
На рисунке представлена структурная схема разработанной методики формирования неизмеряемых параметров двигателя по комплексу значений измеряемых параметров. При разработке методики автор опиралась на рекомендации, изложенные в материалах [1].

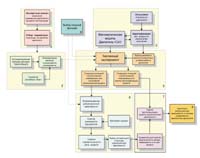Методика построения регрессионной зависимости состоит из следующих этапов: отбор параметров, влияющих на техническое состояние двигателя в эксплуатации, определение диапазона изменения параметров влияния; формирование ортонормированной статистической матрицы планирования численного эксперимента, которая характеризует парк виртуальных двигателей, имеющих различное техническое состояние; разработка всережимной имитационной математической модели "двигатель-САУ", идентификация модели по результатам натурных испытаний; выбор структуры опорной функции для построения регрессионной зависимости; генерирование исходной информации для построения регрессионной зависимости и проверки ее прогнозирующих свойств на основании численного эксперимента по идентифицированной математической модели в характерных высотно-скоростных условиях эксплуатации и на назначенных режимах работы двигателя; формирование регрессионной зависимости, оценка значимости аргументов, минимизация структуры по заданным критериям оценки; оценка чувствительности регрессионной модели к точности входной информации; оценка прогнозирующих свойств регрессионной зависимости; сравнительный анализ результатов расчетов искомой функции по регрессионной зависимости и математической модели; адаптация регрессионной зависимости в системы управления и диагностики двигателя.

На основании статистического материала, полученного при эксплуатации двигателей, выделены параметры газовоздушного тракта и узлов двигателя (параметры влияния), ответственные за трансформацию характеристик двигателей при выработке ресурса; определены их возможные минимальные и максимальные отклонения от номинальных и диапазоны варьирования.
С использованием принципов теории планирования эксперимента: рандомизации, центрирования, кодирования и ортонормирования с помощью известного математического метода Грама-Шмидта в целях трансформирования факторного пространства в единичную гиперсферу построен многофакторный статистический ортонормированный план влияния для проведения расчетных экспериментов с применением математической модели "двигатель-САУ".

Этот план представляет собой матрицу размерности (mxn), для формирования которой проведены следующие операции: 1) Трансформирование многофакторного пространства Х в единичную гиперсферу путем нормирования переменных - параметров влияния. 2) Случайная выборка (рандомизация) значения параметра из диапазона варьирования с выполнением условия равновероятной выборки, что позволило в дальнейшем компенсировать влияние систематических ошибок при проведении численного эксперимента. 3) Обеспечение линейной независимости факторов, равенства нулю скалярного произведения m-размерных векторов-факторов, входящих в план, с помощью ортогонализации.

Таким образом, была получена ортонормированная случайная выборка в факторном пространстве с равновероятным распределением вектора X_i, i = 1, 2, …, n, которая образует матрицу планирования эксперимента размером [mxn]. Каждая строка этой матрицы представляет собой уникальный виртуальный двигатель с присущими только ему измененными характеристиками узлов.

Выбираются характерные высотно-скоростные условия и режимы работы двигателя, отражающие полный спектр условий эксплуатации и режимов его работы (от Н=0 до Н_max и от M=0 до M_max; от "малого газа" до "полного форсажа"), в которых проведены расчетные эксперименты для генерации статистических матриц обучающей и экзаменационной последовательностей, состоящих из n столбцов независимых факторов (значений измеряемых параметров) и одного столбца искомой функции.

В качестве опорной (целевой) функции для формирования регрессионной зависимости, связывающей искомую функцию с независимыми факторами, принята степенная функция вида: Y= c₀ПХ^а,

где с₀ - постоянный коэффициент;

а - показатель степени i-го аргумента.

Такой вид целевой функции выбран не случайно: многие процессы в газотурбинном двигателе описываются уравнениями, представляющими произведения степеней компонентов векторов параметров (уравнения расходов газа, степени сжатия и расширения в лопаточных машинах, уравнение мощностей и др.). Логарифмирование этого выражения приводит к линейному уравнению: lnY_j=C_0j+ (a_ij lnX_i),

где lnY_j - матрица прологарифмированных значений целевых функций,

lnX_i - матрица прологарифмированных значений измеряемых параметров,

C_0j, a_ij - матрицы постоянных коэффициентов.

Коэффициенты C_0j и a_ij определяют методом наименьших квадратов по результатам численного эксперимента, проведенного с использованием математической модели "двигатель-САУ" и материалов экспериментальных испытаний двигателя.

Одним из основных достоинств аппроксимации температуры газа степенной функцией является относительно небольшое число коэффициентов (n+1), тогда как традиционная аппроксимация полиномом хотя бы второго порядка требует значительно большего числа коэффициентов.

Для примера приведем регрессионную зависимость, полученную для одного из перспективных двигателей.

Регрессионная модель определения Т*_Г имеет экспоненциальный вид, которая зависит от T_ВX - относительной температуры воздуха на входе в двигатель, T_X - относительной температуры воздуха перед компрессором, T₂ - относительной температуры воздуха за компрессором и т.д. Суммарная относительная погрешность определения параметра Т*_Г по регрессионной модели включает в себя:

Ошибка измерения Т*Г при современной точности измерений составляет ± 6,06 К.

Были рассчитаны показатели точности вычисления по регрессионной модели для Т*_Г, которые характеризуются значениями:

Суммарная среднеквадратичная ошибка определения среднемассовой температуры газа по регрессионной модели составляет ΔТ_{Г регр} = ± 7,8 К при доверительной вероятности р = 0,95.

Литература

1. Добрянский Г.В., Алексеев В.А. и др. Статистические алгоритмы для эксплуатации газотурбинных двигателей по техническому состоянию. - М.: "Двигатель", 2002, № 3 (21). С. 22-24.

2. Адлер Ю.П., Маркова Е.В., Грановский. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.

[Напоминаем, что Интернет-вариант статьи сильно сокращен. Ред.]