
|
ТУРБУЛЕНТНОСТЬ
ЛЕОНАРДА ЭЙЛЕРА.
АЛЬТЕРНАТИВНАЯ ИНТЕРПРЕТАЦИЯ
Юрий Михайлович Кочетков, д.т.н.
 Более
двух с половиной столетий газодинамики пользуются уравнениями Эйлера.
В своем классе это уравнения, которые описывают практически все возможные
случаи турбулентных течений жидкости, газа и плазмы. При помощи уравнений
Эйлера определяются структура газового потока, интегральные характеристики
потока, начальные и граничные условия для сопряженных задач теплообмена,
электро-, и магнитодинамики, задач для низкотемпературной плазмотехники
и техники генерации электронных и лазерных пучков. Такая востребованность
уравнений обусловлена их универсальностью, а незатухающий интерес к
ним постоянно побуждает к анализу, в процессе которого открываются все
новые и новые свойства.
Более
двух с половиной столетий газодинамики пользуются уравнениями Эйлера.
В своем классе это уравнения, которые описывают практически все возможные
случаи турбулентных течений жидкости, газа и плазмы. При помощи уравнений
Эйлера определяются структура газового потока, интегральные характеристики
потока, начальные и граничные условия для сопряженных задач теплообмена,
электро-, и магнитодинамики, задач для низкотемпературной плазмотехники
и техники генерации электронных и лазерных пучков. Такая востребованность
уравнений обусловлена их универсальностью, а незатухающий интерес к
ним постоянно побуждает к анализу, в процессе которого открываются все
новые и новые свойства.
В предыдущей статье было показано, что для случая несжимаемой жидкости или газа уравнение Навье-Стокса превращается в уравнение Эйлера в трех случаях: величина коэффициента вязкости стремится к нулю, значение числа Рейнольдса стремится к бесконечности, лапласиан от вектора скорости равен нулю.
Любое из перечисленных выше условий, так или иначе, характеризует турбулентность несжимаемых потоков. Другими словами, каждое из этих условий определяет все четыре основных вида движения сплошной, деформируемой, подвижной среды: поступательное, волновое (колебательное), вращательное и деформационное (кручение).
При рассмотрении сжимаемой среды условия несколько изменяются и приобретают более сложный внешний вид и физическую трактовку.
 Несжимаемой
среда считается в том случае, когда ее плотность практически не изменяется.
Если количественное изменение относительного приращения плотности определять
по известной формуле:
Несжимаемой
среда считается в том случае, когда ее плотность практически не изменяется.
Если количественное изменение относительного приращения плотности определять
по известной формуле:![]() ,
где М - число Маха, то допустимая величина, не меньше полпроцента, например,
для продуктов сгорания РДТТ будет реализована при скоростях истечения
не более 100 м/с. Для других ситуаций эта величина может изменяться
в более широком диапазоне скоростей. Так, например, для водорода она
не более 150 м/с, а для гексафторида урана - менее 10 м/с.
,
где М - число Маха, то допустимая величина, не меньше полпроцента, например,
для продуктов сгорания РДТТ будет реализована при скоростях истечения
не более 100 м/с. Для других ситуаций эта величина может изменяться
в более широком диапазоне скоростей. Так, например, для водорода она
не более 150 м/с, а для гексафторида урана - менее 10 м/с.
В противном случае среда считается сжимаемой. Часто говорят о двух видах течений: о несжимаемых течениях, понимая под этим обширный класс существенно дозвуковых течений, и о сжимаемых течениях, понимая под этим течения со скоростью, сравнимой со скоростью звука или превосходящей ее.
Поскольку плотность является обратной величиной относительного объема, то и его относительное изменение так же близко к нулю. Другими словами, для несжимаемых сред дивергенция скорости относительного изменения объема (или абсолютной скорости потока) равна нулю divV=0. Это векторное уравнение является газодинамическим условием несжимаемости и его можно использовать для дальнейшего анализа уравнений Навье-Стокса и Эйлера.
В самом общем виде уравнение Навье-Стокса может быть получено из реологического уравнения состояния, связывающего напряжения в подвижной деформируемой среде с деформациями этой среды. В математической трактовке - тензор напряжений связывается с тензором деформаций при помощи постоянных коэффициентов Ламе. При переходе от записи реологического уравнения в тензорном виде соответственно к гидродинамической (газодинамической) записи были использованы две гипотезы.
-
Гипотеза (закон трения) Ньютона о пропорциональности касательных напряжений скоростям деформаций. При этом был введен коэффициент пропорциональности, названный коэффициентом динамической вязкости µ (условно первая вязкость).
-
Гипотеза Стокса о взаимосвязи второй, объемной вязкости
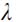 с первой динамической вязкостью µ, выражающаяся в виде
с первой динамической вязкостью µ, выражающаяся в виде
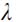 = -2/3µ. При этом,
хотя Стокс теоретически обосновал свою зависимость, она все еще подвергается
обсуждению.
= -2/3µ. При этом,
хотя Стокс теоретически обосновал свою зависимость, она все еще подвергается
обсуждению.
 С
учетом обеих гипотез, а также того широко известного факта, что для
большинства газов (исключение составляют реагирующие двухфазные смеси)
коэффициент второй вязкости
С
учетом обеих гипотез, а также того широко известного факта, что для
большинства газов (исключение составляют реагирующие двухфазные смеси)
коэффициент второй вязкости ![]() точно или приближенно равен нулю, в уравнении Навье-Стокса для сжимаемой
среды, в отличие от несжимаемой, появляется дополнительный член: 1/3µgrad(divV).
Дополнительный член пропадает при использовании условия несжимаемости.
точно или приближенно равен нулю, в уравнении Навье-Стокса для сжимаемой
среды, в отличие от несжимаемой, появляется дополнительный член: 1/3µgrad(divV).
Дополнительный член пропадает при использовании условия несжимаемости.
Если правая часть уравнения Навье-Стокса,
зависящая от вязкости, равна нулю, то уравнение превращается в уравнение
Эйлера. Это очевидный факт. Далее путем несложных преобразований получаем
альтернативную интерпретацию (АИ) уравнения Эйлера: ![]() .
.
Такая запись адекватно описывает поле скоростей эйлеровой среды, то есть среды без вязкого трения. Очевидно, что это уравнение включает все составляющие суммарного турбулентного движения, в том числе кручение потока.
Физически вектор ![]() является аналогом кручения. В самом простейшем случае его можно представить
как вектор угловой скорости, вращающийся относительно неподвижного центра.
Линии тока при таком движении располагаются аналогично проводам в катушке
индуктивности с кольцевым сердечником. Направление этого вектора всегда
будет перпендикулярно к вектору угловой скорости. В свою очередь, угловая
скорость будет перпендикулярна абсолютной скорости течения v.
Про взаимное расположение векторов v и
является аналогом кручения. В самом простейшем случае его можно представить
как вектор угловой скорости, вращающийся относительно неподвижного центра.
Линии тока при таком движении располагаются аналогично проводам в катушке
индуктивности с кольцевым сердечником. Направление этого вектора всегда
будет перпендикулярно к вектору угловой скорости. В свою очередь, угловая
скорость будет перпендикулярна абсолютной скорости течения v.
Про взаимное расположение векторов v и ![]() можно
пока сказать, что они компланарны.
можно
пока сказать, что они компланарны.
Далее, учитывая, что вектор скорости является производной радиуса-вектора получаем уравнение относительно третьих производных радиуса-вектора по координатам x, y, z.
Такого типа выражение входит в состав важной геометрической характеристики пространственных кривых - кручения. Геометрически кручение определяет меру пространственности кривой. Если кручение равно нулю Т = 0 (Т - кручение), то кривая является плоской, и тогда для ее описания достаточно понятия кривизны.
 Кручение
пространственной кривой в точке М (x, y, z) определяется формулой,
в которую входят три первые производные по всем трем координатам. Все
шесть слагаемых содержат третью производную. Поэтому аналогично тому,
что кривизна ассоциируется со второй производной, кручение ассоциируется
с третьей производной.
Кручение
пространственной кривой в точке М (x, y, z) определяется формулой,
в которую входят три первые производные по всем трем координатам. Все
шесть слагаемых содержат третью производную. Поэтому аналогично тому,
что кривизна ассоциируется со второй производной, кручение ассоциируется
с третьей производной.
Обратное значение кручению - радиус кручения. Например, для винтовой линии радиус кручения является величиной постоянной. Соответственно, скрутка электрических проводов имеет не только постоянную кривизну образующей, но и радиус кручения. Аналогично этому газодинамические скрученные жгуты также имеют постоянные кривизну и кручение.
 Таким
образом, можно отметить, что оба члена уравнения Эйлера (АИ) характеризуют
кручение потока. Становится понятным смысл выражения, отмеченного в
предыдущей статье:
Таким
образом, можно отметить, что оба члена уравнения Эйлера (АИ) характеризуют
кручение потока. Становится понятным смысл выражения, отмеченного в
предыдущей статье: ![]() .
Это выражение означает отсутствие в потоке кручения. И аналогично тому,
как если лапласиан потенциала скорости равен нулю, то течение является
потенциальным, в данном случае течение является дисторсионным (фр. torsion
- скручивание), если лапласиан вектора скорости равен нулю.
.
Это выражение означает отсутствие в потоке кручения. И аналогично тому,
как если лапласиан потенциала скорости равен нулю, то течение является
потенциальным, в данном случае течение является дисторсионным (фр. torsion
- скручивание), если лапласиан вектора скорости равен нулю.
Однако, в общем случае лапласиан
не равен нулю. Его зависимость от трех координат определяет решение
уравнения Эйлера (АИ).
Рассматриваемое уравнение можно представить в виде:![]() . Это векторное уравнение разбивается на три скалярных уравнения:
. Это векторное уравнение разбивается на три скалярных уравнения: ![]() .
.
 Если
известны проекции вектора
Если
известны проекции вектора ![]() ,
а искомыми функциями являются
,
а искомыми функциями являются ![]() ,
то каждое из этих уравнений представляет собой уравнение Пуассона. Аналитическое
решение уравнения Пуассона находится либо через функцию Грина, либо
путем вычисления объемного или ньютонова потенциала. И в зависимости
от ситуации решается либо краевая задача Дирихле, либо задача Неймана.
,
то каждое из этих уравнений представляет собой уравнение Пуассона. Аналитическое
решение уравнения Пуассона находится либо через функцию Грина, либо
путем вычисления объемного или ньютонова потенциала. И в зависимости
от ситуации решается либо краевая задача Дирихле, либо задача Неймана.
Полученная новая альтернативная интерпретация уравнения Эйлера, безусловно,
требует дальнейшего теоретического изучения и дополнительных экспериментальных
иллюстраций. Она открывает возможности представления полей турбулентного
движения жидкостей, газа и плазмы в виде торсионных полей.