ТУРБУЛЕНТНОСТЬ СТРАТИФИЦИРОВАННЫХ ПОТОКОВ

Юрий Михайлович Кочетков, д.т.н.

Наиболее сложный вид турбулентности - это турбулентность стратифицированных потоков. Такой вид турбулентного течения жидкостей, газа и плазмы характеризуется тем, что на границе "смешивающихся" сред возникает сложное сдвиговое течение со скачкообразным изменением параметров на границе: перепадами скоростей, давлений, температур и пр. Скачки параметров приводят к образованию различных устойчивых конфигураций, переходящих от двумерных к пространственным, от ламинарного течения к развитой турбулентности.

Многие задачи практической газовой динамики связаны со стратифицированными потоками (stratification - напластование), то есть с такими потоками, в которых движущиеся друг относительно друга слои жидкости, газа или плазмы обладают различающимися свойствами. По природе своей стратификация бывает различных видов. В метеорологии исследуют относительные потоки воздушных масс, имеющих различные значения температур (тепловая стратификация). При относительном движении газов и жидкостей с различными плотностями также происходит стратификация, которая может приводить к перемешиванию соприкасающихся слоев. Жидкости и газы с одинаковой температурой и плотностью могут быть также стратифицированы, если на границе слоев образуется сдвиговое течение и скорости в этом месте различаются на конечную величину U = U₁- U₂.

Все подобные течения приводят к возникновению турбулентности в областях контактов взаимодействующих слоев. При этом сложность и интенсивность турбулентных образований зависит от параметров, характеризующих сдвиг ( Т, , U и пр.). Учитывая, что термодинамические и газодинамические параметры между собой взаимосвязаны, критерием, характеризующим турбулентное течение, может служить число Рейнольдса, представленное в следующем виде:

Re = U·d/ ,

где d - линейный размер, характеризующий контакт пластов жидкостей или газов;

- кинематическая вязкость условной смеси.

В зависимости от величины числа Рейнольдса можно также судить о мере интенсивности взаимодействия соприкасающихся потоков и о структуре на их границе. При достаточно больших значениях так называемых сдвиговых параметров интенсивность взаимодействия может оказаться весьма существенной. Например, при бреющем полете сверхзвукового самолета над поверхностью моря значения разностей температур, плотностей, скоростей внешней среды и выхлопных газов такие большие, что их взаимодействие приводит к эффекту эжектирования части приповерхностной испарившейся воды выбрасываемыми из сопел струями. Такие процессы можно характеризовать как процессы развитой турбулентности в стратифицированных потоках.

Классическим примером стратифицированных потоков является так называемая неустойчивость Кельвина-Гельмгольца в сдвиговом течении. Эффект демонстрируется на двухслойной жидкости (вода поверх солевого раствора), которая, находясь в прозрачной прямоугольной трубе, внезапно наклоняется. Относительное движение жидкостей с разными плотностями приводит к образованию синусоидальной границы, затем за счет нелинейных свойств вязких потоков, проявляющихся на границе раздела, она деформируется, приобретая форму градиентной волны ("Двигатель", № 5 (47) - 2006). Такие градиентные волны Кельвина-Гельмгольца в дальнейшем разрастаются в регулярные спиральные валики.

Приведенные два примера могут служить крайними ситуациями, характеризующими устойчивые формы турбулентных стратифицированных потоков. Очевидно, что стратифицированные потоки являются наиболее сложными с точки зрения их математического описания по сравнению с любыми другими потоками при внешнем обтекании тел и внутренних течениях в каналах, соплах и диффузорах. Тем не менее такого вида течения могут быть качественно описаны аналогичным образом. Разница в описании сдвиговых течений заключается лишь в отсутствии твердой границы (стенки, мембраны и пр.), а границей является деформирующаяся смежная жидкость, газ или плазма. В процессе течения одну из движущихся деформируемых сред можно рассматривать и как стенку, и как поток. Для определенности наиболее подвижную среду целесообразно считать потоком, а менее подвижную - "стенкой". Так, например, среда с большей скоростью и плотностью может считаться потоком. В случае, когда эти параметры действуют в разных направлениях, при анализе нужно рассматривать их произведение u. Этот параметр характеризует плотность тока m', а его произведение с площадью проходного сечения F - расход: G = uF.

В процессе стратифицированного течения двух и более слоев или, более точно, в процессе их взаимного сопровождения в зависимости от величин параметра u формируются структуры турбулентности по ту и другую стороны. Так, например, турбулентная структура двухслойного течения при завесном охлаждении камер ЖРД или аналогичное течение, сформировавшееся от двухсоставного заряда в РДТТ в разных случаях, может оказаться разной. Плотные, но медленные завесы будут по структуре отличаться от легких и быстрых. Следует отметить, что безразмерным критерием по-прежнему остается критерий Рейнольдса Re.

По аналогии с течениями рабочего тела вблизи стенок машин и аппаратов, течение стратифицированных сред должно рассматриваться как последовательность возможных семи устойчивых конфигураций:

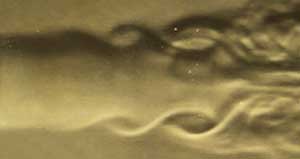Динамику изменения структуры течения стратифицированных потоков лучше всего изучать, анализируя ближний след за профилем крыла или лопатки турбины. Наличие у лопатки спинки и корытца приводит на сходе с нее к образованию стратифицированного потока со сдвиговым профилем скорости. При симметричных условиях обтекания u = 0 и разделительная линия представляет собой либо монотонную кривую, либо прямую. При небольших значениях приращения u форма разделительной линии - синусоидальная, а течение за лопаткой становится волновым. При этом давление и поперечная скорость v периодически меняют знак.

Форма разделительной линии для данного случая может быть получена аналитически методом малых возмущений. При этом необходимо записать уравнение для потенциала возмущений (u, v) однородного двумерного потока при соответствующих граничных условиях.

В случае малых скоростей течения решение ищется методом разделения переменных. Решениями являются колебательная функция вида F = A·sinkx + B·coskx и апериодическая функция.

С учетом малых значений чисел Маха (М) и краевых условий решение для потенциала возмущений на линии разделения потоков может быть записано в виде: = U е(у) coskx.

Форма разделительной линии после интегрирования получится равной: Y= U/U (у) sinkx.

Полученная зависимость качественно характеризует течение в этой области и соответствует экспериментальным результатам.

С увеличением разности скоростей сдвига U, либо в различных средах увеличение плотности тока сдвига приводит к развитию нелинейности и появлению градиентных волн Кельвина-Гельмгольца. Подобную картину течения также можно получить расчетным путем с помощью решений нелинейного уравнения для солитонов типа уравнений Кортевега и де Вриза. При этом потребуется задать граничные условия, учитывающие формирование разделительной линии. Подобные течения будут наблюдаться в двигателях с двухсоставным зарядом, где продукты низкотемпературного топлива, протекающего вдоль стенки сопла РДТТ, будут взаимодействовать с внешним высокотемпературным двухфазным потоком.

Весьма характерным стратифицированным течением являются струи, истекающие либо в спутный поток, либо в затопленную область. На границах струй реализуется сильное сдвиговое течение, и поэтому при различных условиях формируются разделительные линии, соответствующие практически всем названным устойчивым состояниям. При помощи таких течений моделировались процессы в газофазной ядерной энергодвигательной установке.

В настоящее время решение проблемы турбулентности стратифицированных потоков требует своего завершения. Многие практические задачи, связанные со сдвигом параметров в двухслойных структурах ожидают новых идей. Для подтверждения теоретической мысли требуются новые изящные эксперименты, а для правильной постановки экспериментов необходимы нетрадиционные математические решения.