УДК 621

ОПТИМИЗАЦИЯ ФОРМЫ ЛОПАТКИ ГАЗОВОЙ ТУРБИНЫ ПРИ ТРАНСЗВУКОВОМ ТЕЧЕНИИ В МЕЖЛОПАТОЧНОМ КАНАЛЕ

ФГУП "ЦИАМ им. П.И. Баранова":
Франческа Александровна Слободкина, д.ф.-м.н., профессор
Виталий Владимирович Малинин, к.ф.-м.н.
Алексей Владимирович Малинин, инженер-конструктор

 

Методами математического моделирования исследуется обтекание решетки профилей газовой турбины при трансзвуковом течении в межлопаточном канале, определяются области отрыва пограничного слоя на поверхности профиля, проводится модификация формы профиля с целью уменьшения области отрыва, уменьшения потерь и интенсивности вихреобразования.

Mathematical modeling of transonic flow in gas turbine blade cascade is investigated. Proposed approach allows prediction of boundary layer separation zones location. Blade profile optimization is performed to damp separation, decrease cascade losses and minimize vortex formation intensity.

Ключевые слова: решетка профилей, невязкое и вязкое газодинамическое течение, отрыв пограничного слоя, вихреобразование.

Keywords: cascade, inviscid and viscous gas flow, boundary layer separation, eddy generation.

Предлагаемая статья представляет собой развитие предыдущих исследований, изложенных в работе [1] и связанных с оптимизацией течения в турбинной решетке. Здесь также объектом исследования является решетка профилей газовой турбины в потоке вязкой сжимаемой жидкости, но при трансзвуковом течении в межлопаточном канале. В таком течении отрыв пограничного слоя происходит при торможении потока в сверхзвуковой области на спинке профиля с замыкающим скачком уплотнения.
Цель исследования состоит в поиске такой геометрии профиля, при обтекании которого уменьшится зона отрыва, что приведет к уменьшению потерь и, следовательно, повышению коэффициента эффективности устройства.

В работе используются два математических метода:

1. Метод численного расчета обтекания решетки профилей на основе уравнений газовой динамики для идеального газа с последующим вычислением характеристик пограничного слоя и определением зоны отрыва потока на основе критериев подобия [2, 3].

2. Метод численного расчета обтекания решетки профилей на основе уравнений Навье-Стокса для вязких турбулентных течений [4].

Два выбранных метода применяются последовательно следующим образом. На первом этапе на основе многовариантного расчета невязких течений находится приближенное оптимальное решение. На втором этапе полученные результаты проверяются и уточняются по методу 2. Такой подход дает возможность значительно сократить время счета по сравнению с решением задачи только по методу 2.

В данной работе моделируются трансзвуковые режимы течения в решетке профилей с образованием замкнутой сверхзвуковой зоны с отрывом потока. Деформацией профиля удалось в несколько раз сократить область отрыва и снизить потери. Сравнение численных решений с соответствующими экспериментальными результатами подтверждает возможность использования выбранных математических моделей для решения поставленной задачи.

Постановка задачи для трансзвуковых течений в межлопаточных каналах турбинной решетки

В качестве исследуемой решетки профилей рассмотрим плоскую турбинную решетку такую же, как в [1], для которой имеются экспериментальные газодинамические характеристики. Предполагается, что:

- рабочим телом является воздух (рассматриваемый в методе 1 как невязкий сжимаемый газ, в методе 2 - как вязкий сжимаемый газ);
- граничные условия на поверхности лопатки - равенство нулю нормальной составляющей скорости потока (условие непротекания) и адиабатическая стенка - для первого метода, равенство нулю скорости - для второго метода;
- угол входа потока равен 54° от вертикали (ось Y) т.е. поток направлен под углом 36° к продольной оси X.

Приведем результаты расчета обтекания решетки профилей - исходных и полученных оптимизацией, целью которой было снижение потерь в решетке путём уменьшения области отрыва потока. Численные результаты получены с использованием уравнений Эйлера [2], а затем - уравнений Навье-Стокса с осреднением по Рейнольдсу для вязкого турбулентного сжимаемого течения [4].

Последняя задача замыкается двухпараметрической k-ω моделью турбулентности. Рассматривается двумерное плоское вязкое течение сжимаемого изотермического газа при обтекании решетки профилей для величины коэффициента скорости λ = 0,73 на выходе из решетки. Такое значение λ обеспечивает в эксперименте трансзвуковое течение внутри межлопаточного канала. Этот вариант течения выбран потому, что потери, связанные с отрывом потока в трансзвуковой области наиболее существенны: сверхзвуковая область течения при торможении потока на спинке профиля заканчивается скачком уплотнения.

Взаимодействующий с пограничным слоем скачок вызывает отрыв потока и вихреобразование. Потери в этом случае выше, чем при плавном торможении (как это происходит в дозвуковых течениях).

Условия численной "продувки":

На входе в решетку задаются атмосферные граничные условия, т.е. полное давление Р* = 1атм и Т* = 293 К. На выходе из решетки задается статическое давление, которое рассчитывается через газодинамическую функцию π(λ) и обеспечивает заданное в эксперименте значение λ = 0,73, на верхней и нижней границах расчетной области задается условие периодичности. Это условие, в частности, отличает постановку задачи обтекания решетки профилей от задачи обтекания одиночного профиля [5, 6].

На рис. 1 представлена расчетная область и сетка из 500000 ячеек, разработанная для этой задачи. Сетка содержит сгущение измельченных ячеек вблизи стенок профиля для детального описания процессов в пограничном слое. Учет режимов течения с переходом через скорость звука и торможения в скачке уплотнения также требует увеличения числа ячеек и уменьшения их размера по сравнению с расчетами дозвуковых режимов.

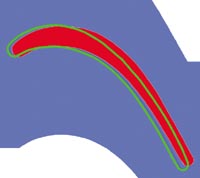На рис. 2 представлена геометрия исходного профиля, заданного в эксперименте (красный профиль), и геометрия оптимизированного профиля (зеленая линия). Оптимизация проведена по методам, описанным в статье [1].

Решение задачи обтекания вязким сжимаемым газом исходной решетки профилей

На рис. 3 - 5 представлены результаты расчета обтекания решетки с исходной геометрией профилей вязким сжимаемым газом при трансзвуковом течении в межлопаточном канале.

На рис. 3 показано распределение числа Маха в поле течения при численной продувке исходной решетки сжимаемым вязким газом. Значение коэффициента скорости на выходе из решетки λ = 0,73. Хорошо виден переход течения через скорость звука на спинке профиля вблизи носика и развитие отрывной зоны. Слева на рисунке дана шкала цветовой гаммы для значений чисел Маха на данном режиме.

На рис. 4 представлено распределение числа Маха вблизи передней кромки профиля в увеличенном масштабе, что дает детальное представление о характере обтекания решетки при трансзвуковом режиме. Рис. 4, 5 отчетливо демонстрируют явление развитого отрыва. Необходимо отметить, что область отрыва ограничена - по мере удаления по спинке к концу профиля поток в некотором сечении снова присоединяется к стенке.

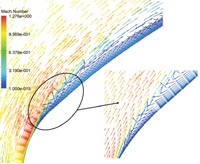На рис. 4 хорошо видна система косых скачков, возникающих в зоне передней кромки при сверхзвуковом потоке и отрывном течении. На рис. 5 представлена структура течения в отрывной зоне с использованием векторов скорости. Цвет и размер векторов соответствуют величине скорости в данной точке. Очевидно, что скачки вызваны торможением потока и взаимодействием с пограничным слоем, а не недостаточной гладкостью профиля. В то же время, в случае оптимизированного профиля, как будет показано ниже, интенсивность отрыва низка, что не приводит к заметной перестройке потока.

На рис. 5 также виден переход течения через скорость звука и образование возвратного течения на спинке профиля, характерного для отрыва потока. Расчет распределения давления подтверждает трансзвуковой характер течения в решетке и наличие отрыва. Сверхзвуковая зона с косыми скачками довольно большая. Замыкающий скачок уплотнения, которым заканчивается сверхзвуковая область, и развитый отрыв приводят к увеличению потерь в межлопаточном канале.

Решение задачи обтекания вязким сжимаемым газом оптимизированной решетки профилей

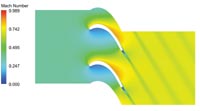Приведем результаты численной "продувки" оптимизированной решетки профилей турбины при трансзвуковом течении в межлопаточном канале.

Постановка задачи и математические модели такие же, как в предыдущем пункте, но профиль решетки модифицирован так, что зона отрыва существенно уменьшена. Численным решением уравнений Навье-Стокса проверяются газодинамические свойства течения в модифицированной решетке. По аналогии с представленными выше результатами здесь демонстрируется поле распределения числа Маха (рис. 6) при обтекании решетки оптимизированных профилей.

Выигрыш в сокращении зоны отрыва заметен при сопоставлении рис. 4 и рис. 7, где в увеличенном масштабе представлены области отрыва потока вблизи передней кромки профиля. Такое подробное описание сложного течения возможно только при адекватном построении расчетной сетки и выборе численной схемы в этой области.

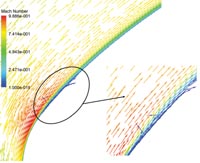Из результатов, представленных на рис. 6 следует, что течение всюду дозвуковое, отрыв на передней кромке практически отсутствует. Особенно четко значительное уменьшение зоны отрыва видно на рис. 7 и рис. 8, где результаты приведены в увеличенном масштабе. Интенсивность отрыва существенно снижена по сравнению с результатами для экспериментального профиля. Распределение относительного напряжения на профиле, представленное на рис. 10, подтверждает результаты, продемонстрированные на примере числа Маха. Оптимальная деформация профиля привела к тому, что течение всюду стало дозвуковым (рис. 11) и отрыв на передней кромке практически отсутствует (рис. 10).

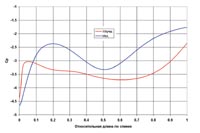
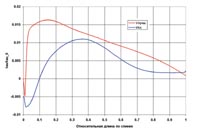Сравнение значений характеристик решеток профилей для двух турбин, приведенных на рис. 7 - 10, дают не только качественное, но и количественное представление о выигрыше при использовании оптимизированного профиля. Так, например, зона отрыва на исходном профиле составляет ~ 39,4% от длины спинки, в то время как на оптимизированном профиле зона отрыва занимает только 7,5% длины спинки. То есть длина зоны отрыва в результате оптимизации сократилась в 5,25 раза. Сверхзвуковая область на исходном профиле занимает ~ 24,2% длины спинки, в то время как течение в оптимизированной решетке полностью дозвуковое (рис. 11). Это тот результат, к которому обычно стремятся конструкторы турбин. Распределение скорости по спинке оптимизированного профиля более равномерное, чем на исходном профиле, что также благоприятно сказывается на характеристиках турбины. И, наконец, сравнение распределения величин С_р для двух исследованных профилей (рис. 9) показывает, что коэффициент давления на исходном профиле в 1,6 раза больше, чем на оптимизированном при длине по спинке от носика равной 0,2; и в 1,9 раза больше при длине по спинке от носика равной 0,8. Этот факт также свидетельствует об эффективности оптимизации, так как показывает существенное снижение давления на оптимизированный профиль.

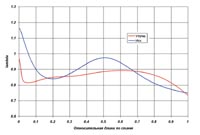Значительное снижение интенсивности отрыва и обеспечение дозвукового режима течения позволили уменьшить потери в оптимизированном профиле по расчетам энтропии на выходе из решетки до 2,7% по сравнению с 3,7% для исходного профиля.

Литература

1. Слободкина Ф.А., Малинин В.В., Малинин А.В. Оптимизация формы лопатки газовой турбины методами математического моделирования. // Двигатель. №5 (77), 2011, с.28-30.
2. Годунов С.К., Забродин А.В., Прокопов Г.П. Разностная схема для двумерных нестационарных задач газовой динамики и расчет обтекания с отошедшей ударной волной. ЖВМ и МФ, 1961, 1, № 6, С.1020-1050.
3. Бам-Зеликович Г.М. Расчет отрыва пограничного слоя. Изв. АН СССР, ОТН, 1954. - 85с.
4. Launder B.E. and Spalding D.B. B. The Numerical Computation of Turbulent Flows // Comp. Meth. Appl. Mech. Eng. - 1974. - V.3. - P. 269-289.
5. Слободкина Ф.А., Малинин В.В., Петров А.Г. Численное исследование возможности построения оптимальной формы лопатки.//Х международная школа-семинар "Модели и методы аэродинамики", Крым, г. Евпатория, 3-12 июня 2010 г., Материалы конференции, С. 157-158.
6. Слободкина Ф.А., Малинин В.В. Оптимизация эффективности работы лопаточных машин путем создания формы лопатки минимального сопротивления. // Российская техническая нефтегазовая конференция и выставка SPE по разведке и добыче 2010. Москва, 26-28 октября 2010 г., Материалы конференции, SPE-135795.