|
УДК 621.431.75
ПРИНЦИП МОДЕЛИРОВАНИЯ ГАЗОДИНАМИЧЕСКИ ЭФФЕКТИВНЫХ ЭЖЕКТОРНЫХ СИСТЕМ ДЛЯ ПЕРСПЕКТИВНЫХ АВИАЦИОННЫХ ДВИГАТЕЛЕЙ
Московский авиационный институт (национальный исследовательский университет) "МАИ", Научно-исследовательский центр новых технологий при МАИ:
Лев Леонидович Картовицкий, доцент, к.т.н.
Антон Владимирович Ципенко, профессор, д.т.н.
Алексей Александрович Яковлев, доцент, к.т.н.
Сформулирован принцип моделирования газодинамически эффективных эжекторных систем для перспективных авиационных двигателей. Выделены основные этапы. Проведены расчеты, демонстрирующие эффективность предлагаемой методики. Проведено сравнение расчетов с результатами экспериментов.
The principle of effective ejection systems modeling for advanced aircraft engines are formulated. Selected milestones. Calculations to demonstrate the effectiveness of the proposed methodology. Comparison of calculation results of experiments.
Ключевые слова: эжектор, авиационный двигатель, 1-D, 2-D, 3-D моделирование, эксперимент, метод крупных частиц, FlowVision.
Keywords: aviation engine, ejector, 1-D, 2-D, 3-D modeling, experiment method of large particles, FlowVision.
Целью моделирования газодинамически эффективных эжекторных систем для перспективных авиационных двигателей (АД) является отработка методики проектирования и определение характеристик эффективной эжекторной системы, т.е. фактически стоит задача оптимизации геометрии и выходных параметров потока из АД по критерию максимальной тяги или расхода. Для решения этой задачи, в связи с огромными временными затратами при использовании сразу 3-D моделирования, предлагается использовать поэтапный подход.
В результате первого этапа определяются диапазоны геометрических размеров и параметров потока эффективной эжекторной системы, для чего определяются проходные сечения основных участков эжектора и параметры потоков на входе в эжектор.
Если требуется рассчитать сопло эжектирующего газа, то на этом этапе сопло рассчитывается по формулам адиабатического истечения невязкого газа или простым 1-D моделям газа с учетом вязкости [1]. Модель сопла определяет площадь критического сечения и площадь сечения на выходе. Степень сжатия эжектора в основном зависит от размера выходного сечения сопла. Критическое сечение сопла желательно выбирать из условия минимизации влияния пограничного слоя в критическом сечении на расход газа.
1-D модели позволяют определить как линейные размеры, так и диаметральные сечения. Осевые размеры и углы раскрытия и сужения конических элементов конструкции эжектора вычисляют, используя эмпирические зависимости (характеристики отрыва потока). Например, следует учитывать рекомендации:
D4 = (1,6...2,0)D3, l2/D3 = 1,0...2,9, (l1 + l2)/D3 = 4,6...6,6,
где D4 - диаметр выхода диффузора эжектора, D3 - диаметр камеры смешения, l2 - длина горла эжектора, l1 - длина сужающегося участка до горла эжектора.
На втором этапе проводится двумерное моделирование без учёта и с учетом вязкости. 2-D моделирование без учета вязкости позволяет уточнить длину эжектора и оценить роль предлагаемых углов сужения эжектора, а с учетом вязкости позволяет уточнить давление запуска, скорректировать диаметр горла и длины характерных участков эжектора. Необходимо отметить, что в численных экспериментах с учетом процесса запуска число Куранта, характеризующее скорость распространения возмущений по расчетной сетке, не должно превышать 1 (возмущения не проходят более одной расчетной ячейки за один шаг по времени). В противном случае нарушаются причинно-следственные связи и численный эксперимент не соответствует реальному процессу (возможны случайные совпадения, но в общем случае соответствия нет). Также в процессе запуска давление в зоне выходного участка эжектора существенно меняется, поэтому границы расчетной области должны быть удалены от выхода эжектора на расстояние, обеспечивающее слабое влияние границ расчетной области (давление вдоль открытых границ должно быть близким к 1 бар). Давление запуска подбирается в ходе различных численных экспериментов.
На этом этапе возможно получение дополнительной информации, касающейся условий эксплуатации. В частности, можно оценить максимальные температуры и выбрать соответствующие материалы и/или систему охлаждения.
При необходимости, например, для несимметричных конструкций или скоса внешнего потока, проводится 3-D моделирование с учетом вязкости. Здесь рекомендуется использовать какой-либо коммерческий (Fluent, FlowVision, ANSYS) или открытый (OpenFoam) пакет для газодинамических расчетов. Целью этих расчетов может быть лишь улучшение отдельных элементов конструкции. Если выяснится, что при 3-D моделировании получено существенное снижение от выбранных (требуемых) показателей эффективности, то необходимо будет снова (глобальная итерация) пройти всю цепочку 1-D-2-D-3-D с учетом изменений в граничных условиях (вход-выход эжектора), выявленных при 3-D моделировании.
Такая технология требует значительных временных затрат на каждый численный эксперимент, но позволяет повысить достоверность результатов, исключив ряд факторов, нарушающих соответствие реального и моделируемого процессов.
Приведем иллюстрацию работы предлагаемого алгоритма на различных этапах.
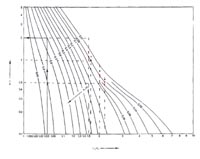Для первого этапа в качестве примера был проведен расчет оптимальных эжекторов для воздуха в качестве эжектирующего и эжектируемого газов при давлениях, соответствующих реальным промышленным эжекторам. Из рис. 1 видно, что 1-D модели дают более оптимистичный коэффициент эжекции по сравнению с реальной конструкцией.
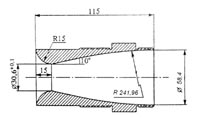
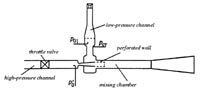Для демонстрации результатов работы на втором этапе в качестве тестового использовался эжектор, описанный в работе [2]. Схема эжектора приведена на рис. 2, размеры сопла рабочего газа (воздух) приведены на рис. 3.
Для данного устройства результаты 1-го этапа показали хорошее соответствие с характеристикой реального эжектора (рис. 4), а результаты второго этапа показали несколько худшую степень повышения полного давления, так как неустойчивый режим работы эжектора возник при переходе от 13 атм в форкамере к 14 атм. Расчет велся в специально разработанной программе с применением метода крупных частиц [3, 4]. Некоторые результаты расчетов по второму этапу представлены на рис. 5.
Таким образом, при использовании модели невязкого газа, точка отрыва более подвижна, чем в реальном потоке, что вполне соответствует физической модели (нет условия нулевой скорости на жестких стенках):
(p01 / p02) = 14/0,3 = 46,7.
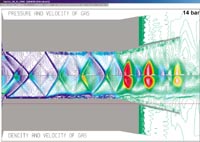
На третьем этапе использовалась коммерческая программа FlowVision. Некоторые результаты приведены на рис. 6, 7. Видно, что сохраняется практически полная осевая симметрия течения, за исключением небольших колебаний отрывной зоны в диффузоре.
Сравнение численных результатов, полученных по предлагаемой технологии, с параметрами известных из научно-технической литературы реальных эжекторов показало хорошее соответствие расчетных и экспериментальных данных. Можно считать, что предлагаемая методика работоспособна и может применяться при проектировании реальных эжекторных систем перспективных АД.
Стоит отметить, что диффузор, как элемент конструкции, который повышает давление, не имеет смысла использовать на летательном аппарате, однако он нужен при наземном использовании АД в качестве энергетической установки.
Таким образом, можно сформулировать следующие принципы моделирования эжекторных систем перспективных АД:
- поэтапное моделирование с последовательным прохождением глобальными итерациями по цепочке 1-D - 2-D - 3-D модели;
- обязательное моделирование переходных и колебательных процессов во всех элементах эжекторной системы, включая сопло рабочего газа;
- учет влияния внешних конструктивных элементов планера и АД на параметры эжектируемого потока как граничных условий.
Литература
1. Abramovich G.N. Applied Gas Dynamics, Moscow: Nauka, Fifth edition, v.1, 1991, ISBN 5-02-014015-5
2. Аркадов Ю.К. Новые газовые эжекторы и эжекционные процессы // -М.: Изд-во Физико-математической литературы, 2001. - 336с.
3. Белоцерковский О.М. Численное моделирование в механике сплошных сред. 2-е изд., переработанное и дополненное. - М.: Физматлит, 1994, 448 с.
4. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. Вычислительный эксперимент. - М.: Наука, 1982, -392 с.
Связь с автором: tempero.m@gmail.com