|
УДК 621.81:539.4:621.89
РАСЧЕТНО-ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ ПРИ ОТНОСИТЕЛЬНОМ ОСЦИЛЛИРУЮЩЕМ ДВИЖЕНИИ ДЕТАЛЕЙ
ФГУП "Центральный институт авиационного моторостроения им. П.И. Баранова":
Борис Федорович Шорр, главный научный сотрудник, д.т.н.
Александр Николаевич Стадников, ведущий конструктор
Николай Николаевич Серебряков, инженер
Предложен способ расчетно-экспериментального определения коэффициентов трения между контактирующими деталями при их относительном осциллирующем движении и приведены результаты определения коэффициента трения между колеблющейся пластиной из титанового сплава и стальной балкой, проанализированы основные факторы, влияющие на величину коэффициентов трения.
The design-experiment method is offered for definition of friction coefficient between contacting components in case of their relative oscillating motion, results of friction coefficient definition are given for titanium plate and steel beam, governing factors influencing on friction coefficient value are analyzed.
Ключевые слова: сухое трение, коэффициент трения, контактирующие поверхности, осциллирующее движение.
Keywords: dry friction, friction coefficient, contacting surfaces, oscillating motion.
Введение
При создании современных газотурбинных двигателей одной из актуальных задач продолжает оставаться предупреждение усталостных повреждений рабочих лопаток. Важнейшим фактором, ограничивающим уровень напряжений, является демпфирующая способность лопаток. Одним из эффективных способов их снижения является введение специальных демпфирующих устройств, принцип действия которых основан на рассеянии энергии силами сухого трения при относительном движении контактирующих поверхностей.
Для решения задачи динамики контактирующих тел определяющим фактором является величина коэффициента трения между контактирующими поверхностями. В ограниченном числе работ экспериментального характера коэффициенты трения многие годы определялись при однонаправленном смещении трущихся пар, в то время как демпфирование в узлах турбомашин происходит при относительном осциллирующем движении контактирующих деталей. В экспериментах В.Я. Касьяненко и В.А. Скибина [1] было показано, что в этих условиях значения коэффициентов трения существенно возрастают и даже могут превысить единицу. Этот факт нашел подтверждение и в некоторых последующих экспериментальных работах [2].
Для получения объективной оценки величин коэффициента трения целесообразно определять различными методами.
Проведение таких исследований требует разработки специальных методик испытаний и соответствующих устройств. В настоящей работе отражены некоторые результаты исследований авторов в указанном направлении.
1. Устройство для экспериментального определения коэффициентов трения в осциллирующей контактной паре
1.1. При разработке устройства было поставлена цель обеспечить возможность независимого изменения в достаточно широких пределах указанных выше параметров: частоты колебаний, размаха скоростей при колебаниях и нормальной статической силы, сдавливающей контактную пару.
С этой целью было предложено использовать следующий принцип действия устройства. Контактная пара образовывается путем переменного контакта двух деталей, из которых одной придается кинематическое возбуждение от электродинамического вибратора на резонансной частоте, а вторая прижимается к одному из участков первой детали с варьируемым измеряемым усилием. В процессе испытания проводится цифровая запись сигнала от тензорезистора, наклеенного на возбуждаемую деталь, при различных условиях испытания.
1.2. В качестве первого этапа исследований была выбрана контактная пара в виде вибрирующей консольной пластины из титанового сплава ОТ4-1 и прижимающаяся к ней упругая балка круглого поперечного сечения из стали Ст3. Приспособление приведено на рис. 1.
Пластина 1 закрепляется консольно в жесткой рамке 2. Толкатель передает динамическую нагрузку от вибростенда 3 к пластине 1, упругая балка 4, прижимается к колеблющейся пластине и фиксируется в приспособлении двумя жесткими штангами, которые позволяют регулировать положение балки относительно пластины по месту их контакта и обеспечивают первоначальный контакт без прижимающей силы.
Прижатие упругой балки 4 к пластине в установленной точке осуществляется через динамометр, по которому контролируется сила прижатия в контакте, которая непосредственно не измеряется. Далее под "силой прижатия" условно понимается сила по показаниям динамометра.
2. Порядок проведения эксперимента
2.1. Установившиеся колебания консольной пластины длиной 90 мм без контакта с балкой возбуждались на электродинамическом стенде по первой изгибной форме с частотой 221 Гц. Задаваемая величина переменных напряжений (например, 50 МПа) контролировалась по тензодатчику, наклеенному на пластину на заданном расстоянии от заделки.
2.2. Последовательно к упругой балке через динамометр прикладывалась прижимающая нагрузка F, равная 10, 20, 30 и 40 Н.
Для нахождения резонансных напряжений в свободном состоянии и при каждом прижатии частота возбуждения ступенчато изменялась так, чтобы на каждом уровне устанавливались стабильные колебания, для контроля которых проводилась непрерывная запись сигнала с помощью прибора MIC-300.
Заметное демпфирование возникало при очень малых силах прижатия, при которых, как показал Фурье-анализ, практически не было сдвига по резонансной частоте колебаний при разных усилиях прижатия. На рис. 2 приведен пример не отфильтрованной записи сигнала при ступенчатом изменении силы прижатия и расположении упругой балки на расстоянии 25 мм от линии заделки пластины.
2.3. Запись сигнала от тензодатчика фильтровалась от высокочастотных помех, возникающих при возбуждении колебаний электродинамическим вибратором. Из отфильтрованного сигнала выделялись временные промежутки, соответствующие определенному усилию прижатия. Полученные записи сигнала обрабатывались с помощью Фурье-анализа, в результате чего уточнялись получавшиеся при испытаниях резонансные амплитуды напряжений и частоты колебаний. Методика расчетно-экспериментального анализа амплитудно-зависимых характеристик демпфирования в деталях и материалах изложена в работе [5].
3. Расчетное определение коэффициентов трения по результатам эксперимента
С целью математического моделирования наблюдаемого при экспериментах процесса колебаний и определения коэффициентов трения были построены КЭ модели пластины и упругой балки. Пластина считалась консольно закрепленной в рамке толкателя, как это было при проведении эксперимента, а в качестве граничных условий балки была принята ее жесткая заделка в месте ее установки в штангу. Контакт балки и торцевой поверхности пластины моделировался с помощью адаптивных GAP-элементов, методика применения которых для решения подобных задач изложена в работе [3].
Вначале был проведен расчет величин вынуждающих переменных усилий, необходимых для возбуждения требуемого уровня переменных напряжений на резонансной частоте колебаний пластины. Расчет проводился в пакете MSC.Nastran. Собственный логарифмический декремент колебаний свободной пластины был принят согласно соответствующему эксперименту δ = 1%. Расчетная резонансная частота получилась равной 220,4 Гц, что незначительно отличается от зафиксированной при испытаниях резонансной частоты. Для возбуждения резонансных колебаний указанного уровня при δ = 1% потребовалось приложить к пластине переменное распределенное давление с амплитудой р = 105 Па.
Далее были проведены расчеты при возбуждении колебаний пластины найденным распределенным переменным давлением в случае прижатия балки к пластине. На последующих рисунках σ - это отношение резонансных напряжений при контакте к напряжениям в свободной пластине.
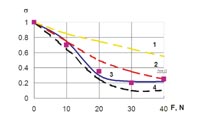Расчеты проводились при тех же прижимающих усилиях 10, 20, 30 и 40 Н, как и в эксперименте. Сопоставление результата расчетов и экспериментов при прижатии балки к пластине приведено на рис. 3. Кривая 3 соответствует экспериментальным измерениям, а штриховые линии относятся к разным расчетным коэффициентам сухого трения между пластиной и балкой: 4 - коэффициенту 0,35; 1 - коэффициенту 0,1; 2 - соответствует коэффициенту 0,2. Из рис. 3 видно, что для исследованной частоты колебаний и нагрузок коэффициент трения лежит в пределах 0,2…0,35.
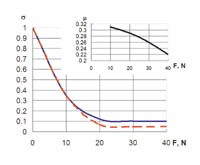Коэффициент трения можно уточнить при разных усилиях поджатия методом перебора так, чтобы точки расчетной и экспериментальной кривой зависимости вибронапряжений от усилия прижатия штанги к образцу при текущем усилии совпали. Для данной системы "пластина-балка" сопоставление расчетной и экспериментальной кривой для коэффициентов трения приведено на рис. 3 (квадратные маркеры), а характер изменения коэффициента трения в зависимости от усилия прижатия балки к торцевой поверхности пластины приведен на рис. 4 (верхний правый угол).
Наблюдаемая на рис. 4 зависимость коэффициентов трения от нормальной нагрузки в области упругого контакта коррелирует с данными работ [4].
Дополнительная проверка характера коэффициента трения может быть проведена с помощью экспериментальной кривой, полученной при прижатии балки к пластине на другом выбранном расстоянии. На рис. 4 (основное поле) сплошная линия относится к результатам эксперимента при х = 35 мм, пунктирная линия - к расчету для того же расстояния х = 35 мм, но с использованием коэффициентов трения, полученных по данным испытания при х = 25 мм. Близость кривых указывает на то, что коэффициент трения слабо зависит от амплитуды относительной скорости осциллирующей пары. Расчет коэффициента трения также можно дополнительно уточнить, если учесть, что внутреннее трение в материалах носит не линейно-вязкий, а амплитудно-зависимый характер [5].
Выводы
Результаты работы позволяют рекомендовать предложенную методику и устройство для исследования влияния частоты и амплитуды относительного движения, температуры в области контакта, усилия прижатия с учетом амплитудно-зависимых характеристик материала исследуемых деталей и других факторов на величину коэффициента сухого трения между контактирующими деталями.
Литература
1. Динамика авиационных газотурбинных двигателей; [под ред. д.т.н., проф. И.А. Биргера и д.т.н., проф. Б.Ф.Шорра]. - М.: Машиностроение, 1981. - 232 с.
2. C.W. Schwingshakl, E.P. Petrov, D.J. Ewins. Validation of test rig measurements and prediction tools for friction interface modelling. Proc. of ASME Turbo Expo 2010, GT2010-23274, 2010, -P. 10;
3. Sang H. Lee, T.L. Lin Self-adaptive GAP/Friction Element in MSC.Nastran, MSC World Users Conference, Los Angeles, 1991, -P. 30;
4. Геккер Ф.Р. Динамика машин, работающих без смазочных материалов в узлах трения. - М.: Машиностроение, 1983. -168 с.;
5. Шорр Б.Ф., Серебряков Н.Н. Расчетно-экспериментальный анализ амплитудно зависимых характеристик демпфирования в деталях и материалах // Проблемы машиностроения и надежности машин. - 2011, №3, С. 91-99.
Связь с автором:
(8-926) 384-7523; shorr@ciam.ru; cap7@yandex.ru