УДК 316.354/776

ОПТИМИЗАЦИЯ ОСЕСИММЕТРИЧНЫХ ЭЛЕМЕНТОВ РОТОРА ГТД СРЕДСТВАМИ ANSYS

ФГУП “ЦИАМ им. П.И. Баранова”
Камалиддин Джамалдинович Каримбаев, начальник сектора
Антон Владелинович Сальников, инженер

 

В данной статье описан макрос на основе ANSYS, который может использоваться для оптимизации осесимметричных элементов ротора (неравномерность температурных полей, широкохордные лопатки, наличие нескольких ступиц, покрывные диски и т.д.). Этот макрос учитывает различные особенности конструкции и ее работы и позволяет создать конструкцию минимальной массы с учетом требований прочности и жесткости.

Used design and optimisation methods for gas-turbine rotor axisymmetric elements leave out of account some structural and operation features (thermal field nonuniformity, long-chord blades, several hub, covered wheels and so on). In this study ANSYS based macro for optimisation of rotor axisymmetric elements capabilities is described. This macro take into account different structural and operation features and allow to find optimal minimum weight design, that meet the requirements of strength and stiffness.

Ключевые слова: оптимизация, прочность, ресурс, диски ГТД.

Keywords: optimization, strength, engine life, gas-turbine engine wheels.

В настоящее время, в связи с существенным увеличением параметров двигателей и требований к ресурсу ГТД, возникает потребность в методиках проектирования роторов турбин и компрессоров минимальной массы, удовлетворяющих ограничениям по прочности и жесткости. Наиболее распространенными на сегодня являются методы, основанные на проектировании дисков, удовлетворяющих заданным запасам прочности по несущей способности (К_В1 и К_В2), дальнейшей проверке полученного варианта конструкции диска на удовлетворение требуемых запасов по малоцикловой долговечности, последующей динамической отстройке от резонансных колебаний и проверке трещиностойкости. Использование таких способов проектирования не всегда позволяет определить наиболее эффективную конструкцию элементов ротора.

В данной статье описаны возможности методики (оформленной в виде  макроса ANSYS) по проектированию элементов ротора ГТД в осесимметричной постановке. Статья написана на основе работ, проведенных авторами в отделении прочности ЦИАМ. На основе данного метода спроектирован ряд элементов роторов.

Запасы прочности К_В1 и К_В2 диска без отверстий в полотне получены из уравнений равновесия сил в меридиональном и цилиндрическом направлениях и определяются по известным соотношениям [1].

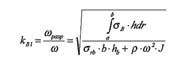
Значения запасов К_В1 и К_В2 определяются нормами прочности. По известному К_В2 из формулы (2) вычисляется толщина полотна диска на каждом радиусе. На следующем шаге выбирается ширина ступицы диска исходя из конструктивных или прочностных требований. Для выбранной ширины ступицы и запаса К_В1 из формулы (1) определяется конфигурация ступицы.

Существуют модификации данного метода с интеграцией с различными решателями МКЭ (ANSYS, Nastran и т. д.), в которых на основе полученных размеров ступицы и полотна диска строятся конечно-элементные модели конструкции и определяются НДС и МЦУ диска. Если спроектированный диск не удовлетворяет требованиям к жёсткости или прочности, то запасы К_В1 и К_В2 изменяют и описанные операции повторяются.

Проектирование с помощью созданного авторами макроса сводится к задаче оптимизации диска по ряду выделенных параметров и заключается в нахождении проекта минимальной массы, который удовлетворяет геометрическим ограничениям конструктивного характера (например, ограничения различных геометрических параметров диска, диктуемые требованиями размещаемости диска в конструкции двигателя), а также ограничениям по прочности и жесткости.

Для решения поставленной задачи применяется встроенный в ANSYS модуль оптимизации [2]. Комплекс ANSYS для решения широкого диапазона проблем оптимизации имеет два метода. Метод приближения подзадачи является эффективным методом нулевого порядка, который может быть эффективно применен для большинства технических проблем. Метод первого порядка основан на чувствительности проекта к варьированию выбранных параметров и более подходит для задач, требующих высокой точности [3].

Для обоих методов комплекс выполняет ряд циклов "расчет - оценка - изменения". Это значит, что выполняется анализ начального проекта, затем результаты сравниваются с указанными критериями проекта и в него вносятся необходимые изменения. Этот процесс повторяется до тех пор, пока не выполнятся все указанные критерии.

В дополнение к двум имеющимся методам оптимизации комплекс ANSYS содержит набор инструментов, которые могут использоваться для увеличения эффективности процесса проектирования. Например, исходные значения данных, полученные на основе оптимизации при помощи случайных чисел, могут служить отправными точками для использования описанных выше методов оптимизации.

В описываемом макросе реализована оптимизация симметричных и несимметричных дисков с одной или несколькими ступицами. При этом количество параметров оптимизации может возрасти в 2...4 раза (в зависимости от количества ступиц), что приведёт к увеличению времени получения оптимального диска с точки зрения заданных критериев (массы, жёсткости, прочности).

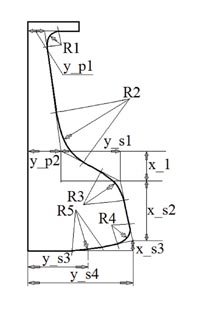Проектирование симметричного одноступичного диска предлагается проводить по 13 оптимизационным параметрам. Выбранные параметры проектирования показаны на рис 1.

Для более быстрого получения решения число параметров оптимизации можно уменьшить, что позволит снизить суммарное число итераций (например, задать радиусы скругления, как постоянные величины). Но недостаточная параметризация иногда не позволяет получить конструкцию диска, которая наилучшим способом удовлетворяет заданным критериям. Следует отметить, что большое число параметров увеличивает время расчёта градиентов целевой функции и суммарное число итераций, а также затрудняет интерпретацию результатов.

При оптимизации диска необходимо учитывать газодинамические, конструкторские и технологические требования. Поэтому определение оптимальных параметров проводится в области допустимых с точки зрения конструкции радиусов обода и расточки диска, а также, ширины и высоты ступицы.

После задания параметров оптимизации с помощью встроенного в ANSYS языка программирования APDL [4] при каждой итерации автоматически создаётся конечно-элементная модель диска с учётом условий работы (температурное поле, частота вращения, инерционные нагрузки от лопаток и выступов диска)[5].
В процессе эксплуатации конструкция подвергается различным комбинациям нагрузок, что приводит к изменению соотношения максимальных напряжений в разных её областях. Поэтому предусмотрена возможность оптимизации с помощью средств ANSYS не по одному режиму нагружения (в большинстве случаев самому тяжёлому), а в условиях всего типового (заданного пользователем) цикла нагружения, в течение которого может происходить изменение условий работы (изменение частоты вращения, температурных полей и т.д.) [6].

Чтобы уменьшить время одной итерации (а значит, и суммарное время определения оптимального проекта), оптимизацию рекомендуется проводить в упругой постановке, предполагая, что оптимальный вариант, полученный в упругой постановке, будет оптимальным и в упруго-пластической постановке. Результаты решения в ANSYS сравниваются с критериями оптимизации. В качестве критерия оптимизации может выбираться масса диска, уровень максимальных напряжений/деформаций или определяемое на основе НДС минимальное значение циклической долговечности.

При несимметричных граничных условиях или при большом осевом размере (при применении широкохордных лопаток) оптимальность конструкции диска связана с использованием несимметрии диска или нескольких ступиц различной конфигурации.

Обычные методы проектирования не позволяют использовать такие особенности конструкции дисков при проектировании.

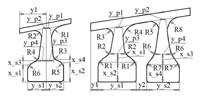В созданном макросе на основе ANSYS реализована оптимизация несимметричных дисков с одним или несколькими полотнами в осесимметричной постановке. На рис 2 показан пример разбиения конструкции несимметричного диска как с одной, так и с двумя ступицами на параметры оптимизации.

Ступицы могут быть как симметричными, так и несимметричными в зависимости от желаемой проработки конструкции.

Оптимизация таких конструкций также проводится в осесимметричной постановке, что позволяет учесть все особенности их нагружения (неравномерность распределения инерционных сил от лопаток вследствие их несимметричности, неравномерность температурного поля, жесткость лопаток и т.д.).

В некоторых случаях необходимо оптимизировать только фрагмент конструкции, при этом остальную часть оставить неизменной. Одним из примеров такого проектирования может служить оптимизация основного диска ТВД вместе с покрывными.

При обычных способах проектирования покрывными дисками либо пренебрегают, либо заранее завышают прочностные запасы основного диска. Оптимизация в осесимметричной постановке позволяет средствами ANSYS автоматически достраивать оптимизируемую конструкцию основного диска с учетом наличия покрывных дисков. Такой подход позволяет подобрать оптимальные конструктивные параметры основного диска при заданных условиях работы.

В конструкции современных турбин высокого давления все чаще появляются покрывные диски, имеющие свою ступицу, с тем чтобы не подгружать основной диск и использовать более экономные системы охлаждения. Поэтому их необходимо проектировать с учётом систем лабиринтных уплотнений и геометрии основного диска.

В зависимости от задачи возможна как одновременная, так и последовательная оптимизация основного и покрывного дисков ТВД с учётом неизменяемых элементов конструкции, введенных конструктором по газодинамическим или гидравлическим требованиям (лабиринтные уплотнения, места соединений и т.д.).

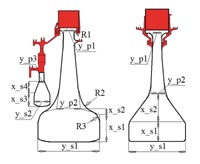На рис. 3 показан схематичный пример разбиения на параметры оптимизации полотен и ступиц покрывного и основного дисков ТВД с учётом постоянных элементов конструкции (помечены красным цветом). Количество параметров оптимизации и схема их выбора может отличаться от представленной в зависимости от желаемой степени проработки конструкции.

Рассматриваемый в данной статье макрос на основе ANSYS позволяет не просто находить оптимальные варианты конструкций элементов ротора ГТД с учётом ограничений на геометрию, прочность и жесткость, но и определять конструкцию с максимальной расчётной долговечностью.

В случае такой постановки задачи минимизируется уровень максимальных напряжений/деформаций с учётом только конструктивных и прочностных ограничений. Масса конструкции при этом не ограничивается. При этом степень увеличения долговечности конструкции, по сравнению с расчетами с учетом ограничения/минимизации массы, зависит от конструктивных ограничений и степени нагруженности элемента ротора и может изменяться в несколько раз.

Такого типа расчёты позволяют определить возможность создания элемента ротора из материала, который удовлетворяет требуемому ресурсу. Если, в результате такой оптимизации конструкцию, удовлетворяющую требуемому ресурсу, создать нельзя, то необходимо менять материал или облегчать условия работы (использовать более лёгкие лопатки, оптимизировать использование охлаждающего воздуха и т. д.).

Литература

1. Биргер И.А., Шорр Б.Ф. Расчет на прочность деталей машин. - М.: Машиностроение, 1993. 640с.

2. Swanson Analysis Systems, Inc. Справочник ANSYS.

3. Реклейтис Г., Рейвиндран А. Оптимизация в технике: В 2-х кн. Кн. 1. - М.: Мир, 1986. 348с.

4. Морозов Е.М., Муйземнек А.Ю., Шадский А.С. ANSYS в руках инженера: Механика разрушения. 2008. 456 с.

5. Басов К.А. ANSYS справочник пользователя. - М.: ДМК пресс, 2005.-640с.:ил.

6. Каримбаев К.Д., Серветник А.Н. Расчёт малоцикловой усталостной долговечности дисков ГТД для реальных условий нагружения летного цикла // Пробл. прочности. - 2009. - С. 129-133.

Связь с автором:

Мобильный телефон: (8-926) 725-6121.

E-mail: kem@ciam.ru