УДК 621.539.822

ПРОБЛЕМЫ НАДЕЖНОСТИ МЕЖРОТОРНОГО ПОДШИПНИКА ПРИ ДИНАМИЧЕСКОМ ВЗАИМОДЕЙСТВИИ РОТОРОВ ДВУХВАЛЬНЫХ ТУРБОРЕАКТИВНЫХ ДВИГАТЕЛЕЙ

ФГУП "ММПП "Салют":
Юрий Борисович Назаренко, начальник бюро динамической прочности, к.т.н.

Лариса Феликсовна Светашова, начальник группы

 

Рассматривается анализ критических частот вращения роторов при ударных нагрузках на опорах, которые формируются при определенных условиях в подшипниках трансмиссии. Ударные нагрузки приводят к качественному изменению критических частот роторов, значения которых отличаются от традиционно определяемых критических частот при синхронных прецессиях. Представлен механизм формирования дополнительных нагрузок на межроторный подшипник от динамического воздействия ротора низкого давления на ротор высокого давления, которое происходит постоянно и не зависит от резонансных явлений.

In this article the analysis of the critical revolution frequency of the rotors influenced by the impact loads on the support bearings, which take place under the certain conditions in the transmission bearings, is presented. The impact loads generate the qualitative changes in the critical frequencies of the rotors, which values differ from the traditional critical frequencies, measured in synchronous processing. The mechanism of the additional loads on the inter-rotor bearing formation is proposed. It is the result of the dynamic impact of the low-pressure rotor on the high-pressure rotor, which takes place constantly and doesn't depend on the resonance pheno-mena.

Ключевые слова: ротор высокого давления, ротор турбины низкого давления, вал, межроторный подшипник, критическая частота ротора, плоские колебания, собственная частота колебаний, прецессия.

Key words: high-pressure rotor, low-pressure turbine rotor, shaft, low-pressure turbine, in-ter-rotor bearing, critical rotor frequency, planar vibrations, self-vibration frequency.

Межроторный подшипник (МРП) является наиболее сложным и проблематичным узлом в трансмиссии двухвальных турбореактивных двигателей.

Одной из основных проблем в оценке его поведения является особенности динамического взаимодействия двух роторов, на стыке которых он находится. Полная картина понимания процессов взаимодействия роторов, особенно с учетом специфики работы межроторного подшипника, и механизмы, описывающие эти процессы, в настоящее время еще не разработаны. Анализ динамического поведения двухроторных систем, выполняемый в программных комплексах высокого уровня, таких как Ansys и Patran, как правило, ограничивается только определением собственных и критических частот вращения роторов при регулярной прецессии.

Исследования, выполненные в последнее время в ФГУП "ММПП "Салют", позволяют по новому взглянуть на данную проблему и найти решение многих вопросов, не имевших своего обоснования до последнего времени. В данной публикации рассматривается анализ критических частот вращения (КЧВ) роторов при ударных нагрузках на опорах, которые формируются при определенных условиях в подшипниках трансмиссии [1]. Ударные нагрузки приводят к качественному изменению критических частот роторов, значения которых отличаются от традиционно определяемых КЧВ при синхронных прецессиях [2]. Также рассматривается динамическое взаимодействие роторов высокого и низкого давления, которое происходит постоянно, независимо от КЧВ, и формирует основные динамические нагрузки на межроторный подшипник [3].

Наряду с динамическими нагрузками от роторов двигателя на тела и дорожки качения могут действовать также динамические нагрузки, которые создает сам подшипник во взаимодействии с роторами. Эти вопросы будут рассмотрены отдельно в последующей публикации.

Динамическое взаимодействие роторов рассмотрим применительно к ротору высокого давления (ВД) и ротору турбины низкого давления (ТНД) двигателя АЛ-31Ф.

Критические частоты вращения роторов при ударных нагрузках на опоре МРП

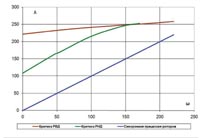
Расчетные зависимости частоты прецессии λ ротора высокого давления (ВД) и ротора турбины низкого давления (ТНД) от частоты вращения валов w, при которых они теряют устойчивость по второй изгибной форме, определены в программном комплексе Patran и приведены на рис. 1.

Как видно из диаграммы, критические частоты вращения роторов находятся выше линии λ = ω , определяющей критические частоты при синхронной прецессии. Критика в данном случае возможна только при несинхронной прецессии, которая практически не реализуется в рабочем диапазоне частот вращения роторов.

В случае возникновения на опорах ударных нагрузок картина кардинально меняется. При синхронной прецессии изогнутая ось вала вращается с частотой вращения ротора и не совершает физических колебаний. Возникновение в этом случае физических колебаний ротора невозможно, так как центробежные силы будут этому препятствовать.

При ударных нагрузках на опорах могут возбуждаться плоские колебания во вращающейся системе координат. Это возможно при сильных воздействиях, действующих синхронно с вращением ротора и попадающих в такт с колебаниями.

Формирование ударных нагрузок на опорах и динамическое поведение ротора рассмотрим на примере ротора ВД на опоре МРП, останавливаясь только на основных принципах формирования ударных нагрузок.

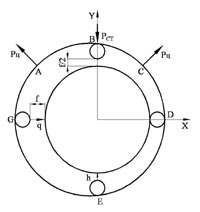В случае, если центробежная сила от дисбаланса ротора ВД ненамного превышает его собственный вес, при определенных условиях возможно зависание ротора ВД, когда в некоторый момент времени ротор не контактирует через ролики с внутренним посадочным кольцом подшипника и валом ротора ТНД, а при контакте происходит удар. Вертикальная составляющая центробежной силы от дисбаланса ротора РЦ, направленная вверх при некотором угле от вертикальной оси (в т. А и в т. C), становится равной силе от собственного веса РСТ (рис. 2). При перемещении центробежной силы (от т. А до т. C) вертикальная составляющая центробежной силы от дисбаланса будет больше силы собственного веса и ротор начнет подниматься.

Вертикальное перемещение ротора ВД за время подъема составит: , где γ- отношение центробежной силы к весу ротора ВД, приходящиеся на заднюю опору; g - ускорение свободного падения; Т - время одного оборота ротора ВД; t₁ и t₂ -время начала и окончания подъема; ξ =2π/Т; Δt = t ₂-t₁.

Если величина подъема не превысит зазор подшипника на вертикальной оси, который составляет половину люфта подшипника (f/2), то при дальнейшем перемещении центробежной силы от вертикальной оси (т. В) до горизонтальной оси (т. D) на ротор ВД будет действовать горизонтальная составляющая центробежной силы от дисбаланса. При этом суммарное горизонтальное перемещение составит: .  (2)

В этой формуле оценивается сближение роторов на горизонтальном диаметре.

Если горизонтальное перемещение превысит люфт подшипника f, то произойдет динамическая посадка ротора на внутреннее кольцо подшипника и вал ТНД.

Коэффициент динамичности, определенный по энергетической концепции, как отношение кинетической энергии ротора ВД Т0 к энергии упругого статического вдавливания U_С [1], составит:

(3)

Для оценки возможности реализации динамической посадки ротора ВД в любой точке и определения коэффициента динамичности нами разработана программа на ЭВМ.

Ударные нагрузки при динамической посадке ротора ВД на горизонтальном диаметре (в т. D) могут в три раза превышать центробежную силу от дисбаланса ротора, а при посадке ротора в точке на 20° выше горизонтального диаметра - в 6 раз.

Такие сильные ударные воздействия на опоре могут возбудить плоские колебания ротора во вращающейся системе координат.

Для сравнения собственных частот колебаний вращающегося и неподвижного ротора на первом этапе рассмотрим уравнения динамического равновесия инерционных и упругих сил вала с одним диском при невращающемся роторе ВД (рис. 3):

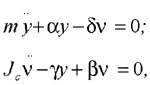
где α и γ- поперечная сила и момент от единичного прогиба вала; δ и β -поперечная сила и момент от единичного углового смещения; J_C - осевой момент инерции диска; y и ν - поперечное перемещение и угол поворота диска.

Решение уравнений (4) будем иметь в виде y = y₀·cosηt  и ν = ν₀·cosηt

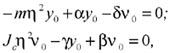(5)

где y₀ и ν₀ - амплитуда поперечных и угловых перемещений плоских колебаний; η - частота плоских колебаний.

При ударных нагрузках для вращающегося диска в системе координат, связанной с ним (совершающей круговое движение с частотой ω), в уравнение (4) необходимо добавить центробежные силы и гироскопический момент:

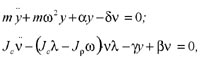(6)

где J_ρ - полярный момент инерции; ω - частота прецессии.

Во вращающейся системе координат ротора ВД в плоскости, где происходят его колебания, будут происходить два вида движения диска.

Первое связано с колебаниями вала, а второе - с его круговым движением. Гироскопический момент диска в этом случае можно определить в квазистатической постановке, т.е. как при синхронной прецессии только при изменяющемся угле поворота диска в соответствии с фазой его колебаний.

Принимая частоту прецессии λ равной угловой скорости вращения вала ω  и полагая для тонких дисков J_C = J_ρ /2, получим значение гироскопического момента
(7)

Подставляя решение уравнений (6), после упрощений (7), получим уравнение плоских колебаний вращающегося ротора

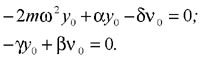(8)

Как видно из уравнений (8), динамический момент диска при плоских колебаниях и гироскопический момент при вращении диска погашают друг друга, а инерционная поперечная и центробежная сила действуют совместно и они равны между собой.

Следовательно, собственные частоты плоских колебаний вращающегося ротора будут соответствовать собственным частотам неподвижного ротора с удвоенной массой всех дисков и лопаток и нулевыми их моментами инерции.

Собственная частота изгибной формы колебаний ротора ВД изделия АЛ-31Ф при ударных нагрузках была определена в программном комплексе Ansys при сохранении жесткостных характеристик дисков и лопаток, при нулевой их плотности, и задании массовых характеристик точечными элементами Mass 21 (рис. 4).

Собственная частота плоских колебаний вращающегося ротора по второй изгибной форме является в то же время и критической частотой ротора ВД и она составляет 186,7 Гц при собственной частоте неподвижного ротора 221 Гц. При этом критическая частота без ударных нагрузок находится намного выше рабочего диапазона вращения и составляет 260 Гц.

Динамическое взаимодействие роторов и формирование нагрузок на МРП

При анализе динамического поведения двухроторных систем и формировании нагрузок на МРП, как правило, учитываются только центробежные силы от дисбаланса ротора ВД, который принимается для двигателей имеющих износ, равным 125 г·см. Такой дисбаланс создает нагрузки на МРП (100% режим) порядка 247 кгс.

Дисбалансы роторов ВД и ТНД равные 125 г·см могут возникать не только при износе двигателей, но и при изменении люфта подшипников в эксплуатации, так как балансировка роторов производится на частотах, гораздо меньших максимальных частот вращения двигателя, и в холодном состоянии.

Кроме этого ротор ВД возбуждает колебания ротора ТНД на межроторной частоте (во вращающейся системе координат ротора ТНД) и создает несинхронную прецессию вала ТНД. По результатам тензометрирования вала ТНД получено, что поперечные перемещения вала могут достигать до 0,44 мм. Однако такая несинхронная прецессия не может возбудить резонансные колебания вала ТНД, а динамическое взаимодействие роторов не создает дополнительных сил на МРП.

В настоящей работе рассматривается возбуждение вынужденных колебаний ротора ВД от ротора НД и механизм возникновения динамических сил на МРП. Влияние динамического воздействия ротора НД на ротор ВД может быть более значительным и определяется отношением податливостей опор роторов НД и ВД.

Радиальная нагрузка от дисбаланса 125 г·см на опоре ТНД при максимальных частотах вращения роторов составляет Р = 145 кгс.

Поскольку опора ТНД является податливой (жесткость опоры  c = 1,4·10⁷ Н/м), под действием центробежных сил от дисбаланса она будет смещаться на величину 0,1 мм и при этом вал ротора будет совершать круговые движения с частотой ω = 1068 рад/с (100% режим).

Круговое движение от вала ТНД через межроторный подшипник и носок ТВД будет передаваться и ротору высокого давления. При этом амплитуда его колебаний на межроторном подшипнике составит U₀ = 0,093 мм.

При перемещении ротора ВД будет возникать максимальная дополнительная радиальная сила

где m - масса ротора ВД, приходящаяся на межроторный подшипник (109 кг); ω - угловая скорость вращения вала ТНД (ω = 1068 рад/с).

Максимальная радиальная сила при воздействии ротора ТНД на ротор ВД возникает, когда собственные круговые колебания ротора ВД и ТНД будут в противофазе, т.е. когда их центробежные силы будут направлены в противоположные стороны и будут повторяться с частотой, равной разности частот роторов ВД и ТНД.

Таким образом, при динамическом воздействии ротора ТНД на ротор ВД возникают динамические силы, которые будут передаваться через МРП и которые более чем в четыре раза превышают центробежные силы от дисбаланса РВД, закладываемые в расчеты МРП.

Литература

1. Назаренко Ю.Б., Светашова Л.Ф. Динамика тел качения межроторного подшипника газотурбинных двигателей при ударных контактах роликов / Научно-технический конгресс по двигателестроению: сборник тезисов. - М., 2010. - С. 144-147.
2. Назаренко Ю.Б., Светашова Л.Ф. Плоские колебания вращающихся роторов газотурбинных двигателей при ударных нагрузках на опорах / Научно-технический конгресс по двигателестроению: сборник тезисов. - М., 2010. - С. 117-120.
3. Колотников М.Е., Назаренко Ю.Б., Иванов А.И., Светашова Л.Ф. Динамика роторов двухвальных турбореактивных двигателей. Проблемы межроторного подшипника / Научно-технический конгресс по двигателестроению: сборник тезисов.- М., 2008. - С. 112.
Связь с автором:
Электронная почта: nazarenkojb@rambler.ru