ФУНДАМЕНТАЛЬНЫЙ ПОДХОД К РЕКОНСТРУКЦИИ МЕХАНИЧЕСКИХ ПОЛЕЙ ДЛЯ ОЦЕНКИ ЭКСПЛУАТАЦИОННЫХ СВОЙСТВ ИЗДЕЛИЙ ОБОРОНПРОМА

Анатолий Алексеевич Сперанский, в.н.с. РГУ нефти и газа им. И.М. Губкина
Константин Львович Захаров, к.ф.-м.н., гл. конструктор НПП "Векторные системы"
Дмитрий Владимирович Малютин, научный руководитель НПП "РЭМ-вибро"

(Продолжение. Начало в № 1 – 2009)

Обращает на себя внимание резкое повышение сложности описания движения при переходе от трансляционных движений, определяемых заданием вектора положения R(t), к спинорным движениям, определяемым заданием тензора поворота P(t). В самом деле, для трансляционных движений достаточно задать всего три вектора: R(t), V(t) = .R(t), W(t) = .R(t), причем любые два из этих векторов легко находятся по третьему. При описании спинорных движений, определяемых собственно ортогональным тензором, ситуация намного сложнее. Тензор поворота допускает множество различных представлений. В настоящее время описание поворотов еще не стало каноническим. Согласно теореме Эйлера любой поворот может быть осуществлен как один поворот вокруг некоторой оси на некоторый угол. Казалось бы, теорема Эйлера полностью решает все проблемы, но это не так, поскольку фактически указан эффективный способ решения только таких задач, в которых ось поворота фиксирована во времени. Однако в большинстве случаев ось поворота меняется во времени, что резко усложняет все построения.

В продолжение рассмотрения доказана одна важная для приложений теорема о представлении тензора поворота, частные случаи которой известны уже много лет, но общая формулировка была предложена П.А. Жилиным только в 1996 г.: "Любой поворот может быть осуществлен в виде композиции поворотов вокруг произвольно выбираемых и фиксированных во времени осей m и n с углами прецессии, нутации и собственного вращения соответственно". Если m = n, то углы называются углами Эйлера, а единичный вектор e выбирается произвольно, но должен быть ортогонален n.

В разных задачах используют различные описания. Например, в современной физике спинорные движения вообще не рассматриваются, хотя некоторые их характеристики все-таки вводятся без упоминания самого спинорного движения. Между тем спинорные движения играют значительно более важную роль в природе, нежели трансляционные движения.

6. Многомерный подход к описанию напряженно-деформированных состояний

Принятие гипотезы сплошности в качестве основы математического описания поведения материалов означает, что поля величин, определяющих свойства материалов, выражаются кусочно-непрерывными функциями координат и времени. Главными из них являются напряжения, являющиеся результатом воздействий, и деформации, являющиеся следствием напряженных состояний. Воздействие поверхностных и массовых сил в соответствии с принципом Коши характеризуется вектором напряжения, а совокупность всех возможных пар векторов напряжений и единичных векторов нормали к поверхности в соответствующих точках приложения векторов напряжений определяет напряженное состояние в этой точке. Для полного описания напряженного состояния в указанной точке достаточно задать векторы напряжений на трех ортогональных площадках, образующих декартову систему координат. Три вектора напряжений, состоящие из трех декартовых компонент каждый, образуют девять компонент векторов напряжений.

Компоненты вектора напряжений, стоящие на главной диагонали, 11, 22, 33, характеризующие растяжение-сжатие, называют нормальными напряжениями, а остальные компоненты, характеризующие сдвиг, называют касательными напряжениями. Пространственный вектор главных напряжений удовлетворяет уравнению эллипсоида, известному под названием эллипсоида напряжений Ламе. Им определяется важнейшее теоретическое свойство механических систем - колебания материальных точек (частиц) сплошных сред, в том числе твердых тел, обусловлены, в общем случае, эллиптическим пространственным характером годографа вектора напряжений в соответствии с характером воздействия и тензорными свойствами материала объекта.

Следствием напряженных состояний являются деформированные состояния. Понятие “деформация” относится к изменению формы континуума от некоторой начальной (недеформированной) конфигурации до последующей (деформированной) конфигурации. Каждая точка объекта имеет шесть степеней свободы, и ее движение определяется мгновенными (синхронными) значениями трех линейных смещений и трех поворотных смещений. Применение тензорного аппарата приводит к тому, что диагональные члены тензора линейных деформаций представляют собой коэффициенты относительного удлинения вдоль осей координат, а недиагональные члены представляют собой коэффициенты сдвигающих деформаций.

Для достоверной оценки диагностических параметров динамической прочности объекта в измерительных точках контурной поверхности необходимо пространственное измерение как поступательных, так и вращательных компонент измеряемых колебательных деформаций в обоснованно выбранной декартовой системе координат.

7. О достоверности измерений диагностических параметров механических систем

Особый интерес вызывает обратная по отношению к предшествующему рассмотрению задача, когда метрологическое средство в измерительной точке преобразует суперпозицию спектра полных колебаний в сигнал, предназначенный для гармонического анализа спектральных составляющих. Принципиально важными являются два фундаментальных обстоятельства.

Во-первых, необходимо обеспечить достоверное измерение виброакустических параметров колебаний механического поля с определенной чувствительностью в заданном диапазоне частот. В мировой практике эта задача решается на основе использования одноканальных скалярных средств измерения (датчиков, вибропреобразователей и приемников), имеющих определенным образом ориентированную относительно собственной конструкции измерительную ось чувствительного элемента. Как правило, измеритель устанавливается на объекте мониторинга, исходя из соображений, соответствующих опыту и знаниям исследователя, в направлении наиболее вероятного воздействия. Незнание точной пространственной ориентации направления вектора измеряемых колебаний относительно измерительной оси приводит к тому, что любое одноканальное средство измеряет некоторую скалярную величину, являющуюся проекцией вектора на его измерительную ось, ориентированную относительно самого вектора случайным образом. Это же относится к системе скалярных метрологических средств, количество которых не всегда влияет на достоверность измерений. Поэтому можно утверждать, что, как правило, измерения пространственных колебаний одноканальными скалярными средствами дают заниженные энергетические оценки процессов.

Во-вторых, необходимо обеспечить синхронное, с учетом фазовых сдвигов связанных пространственных компонент, измерение во времени и пространстве волновых параметров колебаний механического поля с достаточными для достоверной его реконструкции характеристиками аналого-цифровых преобразований. В мировой практике эта задача реализована некорректно. Для особо ответственных случаев, когда требуется точное знание волновых параметров механических колебаний, наиболее продвинутые на мировом рынке фирмы реализуют эту задачу в виде "трехкомпонентных датчиков", представляющих собой комбинацию из трех ортогонально ориентированных в общем корпусе одноканальных скалярных средств измерений. Однако при таком инженерном подходе чувствительные элементы, строго говоря, пространственно, физически и электрически разнесены, и их измерения, как следствие, имеют фазовые рассогласования. На средних и высоких частотах механического диапазона они настолько существенны, что подобные конструкции принято оснащать электронными ортонормализаторами (корректорами, кондиционерами) электрических сигналов. Из этого следует, что, в общем случае, измерение волновых пространственных процессов совокупностью одноканальных скалярных средств снижает достоверность информации и сужает области их применения.

Рассмотрим физическую последовательность процесса прохождения механической волны в сплошной среде объекта мониторинга. Упругие волны, инициируемые источниками гармонических колебаний, возбуждают колебания измерительной точки с закрепленным в ней пространственным (векторным) вибропреобразователем. Диагностические параметры измеряемых колебаний (движения, перемещения, деформации и их производные) отражают синхронную совокупность линейных откликов на воздействия и подчиняются принципу суперпозиции. Параметры этих колебаний передаются на средство измерения вибрации в соответствии с физическими свойствами и прочностными характеристиками объекта мониторинга. Совокупность внешних воздействий на объект С в соответствии с принципом суперпозиции инициирует пространственный спектр напряжений Н волнового механического поля. Напряжения, являясь энергетическим отражением воздействий, в соответствии с упруго-пластическими тензорными свойствами среды Т порождают пространственный спектр деформаций Д.

С учетом информационного системного подхода, векторная виброакустическая метрология, основанная на измерении волновых параметров механических полей, реализует инструментальную метрологическую идею обратного пространственного преобразования Т*. Спектр деформационных откликов Д объекта мониторинга является, в свою очередь, источником адекватного энергетического воздействия на чувствительный пьезоэлемент векторного метрологического средства. Свойства пьезоэффекта в соответствии с тензорными свойствами чувствительного элемента Т* позволяют линейно преобразовать спектр деформаций чувствительного элемента Д*, тождественно соответствующий за счет жесткого крепления спектру деформаций Д объекта в измерительной точке (Д* º Д), в физически адекватный внешним воздействиям Н спектр измеряемых механических напряжений Н*. Механические напряжения чувствительного элемента Н* приводят к образованию электрического заряда, спектральная характеристика С* которого линейно отражает спектр внешних воздействий С (С* = С ). Это находит отражение в концепции векторно-фазового мониторинга механических систем.

Принципиальным отличием пространственного векторно-фазового преобразования от измерений любых комбинаций однокомпонентных скалярных вибропреобразователей является полная адекватность тензорных представлений свойств чувствительных элементов векторных измерительных средств деформационным критериям прочности на основе обобщенных инвариантов тензора напряжений, определяющих реальные свойства материала (конструкции) объекта. Реализован принцип физического подобия вибрационно-диагностических деформационных характеристик векторных средств измерения интегральным прочностным характеристикам напряженно-деформированных состояний объектов исследований в измерительных точках. В общем случае для объективной оценки параметров механических колебаний необходимо и достаточно в измерительных точках определять достоверно шесть связанных временем компонентов вектора или произвольную компоненту (проекцию) и ее пространственную ориентацию относительно направления вектора.

По поводу достоверности измерения волновых параметров механических полей необходимо отметить следующее. Сложилась практика оценки энергетических параметров колебаний средствами измерения линейных поступательных перемещений. Однако из классической механики известно, что колебательное движение материальной точки состоит как из поступательных, так и вращательных или крутильных колебаний. При этом с учетом того, что в общем случае колебания имеют объемный или пространственный характер, для полного описания движения материальной точки необходима пространственно-временная информация о линейных и угловых компонентах, соответствующих выбранным системам координат. При использовании наиболее распространенной в механике декартовой системы координат для полного описания пространственного колебательного движения необходимо располагать достоверной информацией о трех линейных и трех угловых компонентах. Парадоксально, но в некоторых фундаментальных исследованиях (В.В. Фурдуев, E.G. Thurston, Ю.И. Иориш и др.) при измерении пространственных колебаний угловые компоненты рассматривают в качестве паразитной чувствительности линейных компонент к неизмеряемым (вращательным) компонентам вибрации. Такой взгляд можно оправдать только практическим отсутствием метрологических средств одновременного измерения шести компонент колебательного движения - трех компонент поступательных колебаний и трех компонент вращательных колебаний. Бивекторные 6D-вибропреобразователи открывают такую инструментальную возможность.

Особого внимания с точки зрения достоверности и полноты измерения пространственных колебаний заслуживает следующий факт. Пространственно-временная совокупность воздействий и причин (в том числе свойств) порождает во всех точках объекта воздействия, являющегося сплошной средой или твердым телом, непрерывную волновую (полевую) суперпозицию спектра упруго-пластических напряженно-деформированных состояний. Энергетически перенос инициированных воздействием колебаний происходит с ослаблением напряженно-деформированного состояния обратно пропорционально квадрату расстояния r. Поскольку места установки средств измерений (измерительные точки) выбираются из общих конструктивистско-прочностных предпосылок, то, как правило, они никоим образом не связаны с пространственной ориентацией каждого конкретного воздействия. Рассмотрим изложенную ситуацию в плоскости, образованной вектором одного из воздействий А и произвольной измерительной точкой О.

Максимальная величина и направление вектора воздействия силы А в общем случае не совпадает с направлением на измерительную точку и образует с ним определенный их взаимным расположением ракурс R, под которым воздействие проецируется в виде вектора А_R .

При этом воздействие с размахом колебаний 2А представляется в виде суммы двух синхронных (фазированных) векторов: нормальной проекции вектора воздействия а на направление измерительной точки с размахом колебаний 2а и касательной проекции вектора воздействия в с размахом колебаний 2в.

В случае абсолютно твердого изотропного тела измерительная точка О воспроизводит линейный пространственный годограф в виде прямого отрезка с размахом колебаний 2А, ориентированный под углом относительно направления на источник воздействия. Соотношение максимумов векторов определяет угол наклона годографа.

В случае твердого анизотропного тела, измерительная точка О воспроизводит плоский центрированный относительно нее эллиптический 3D-годограф с большой осью в направлении нормальной компоненты напряжений s и нормальной проекции 2а вектора воздействия, пропорциональной 2а/r², и малой осью в направлении касательной компоненты напряжений , касательной проекции 2в вектора воздействия, пропорциональной 2в/r² и ортогональной большой оси эллипса. Величина малой оси эллипса существенным образом определяется относительным сдвигом фаз , отражающим анизотропные свойства объекта мониторинга в измерительной точке.

Из рассмотрения вытекает важнейший для объективного подхода к достоверности измерения параметров колебаний вывод: линейное воздействие возмущения, в зависимости от взаимного расположения относительно измерительной точки, приводит к двум пространственно ориентированным воздействиям: нормальному (трансляционному, линейному, поступательному, и т. д.), характеризующему процессы растяжения-сжатия, и касательному (спинорному, поворотному, вращательному, крутильному и т.д.), характеризующему сдвиговые процессы. При отсутствии вращения физический смысл образования компонентами тензора деформаций состоит в том, что они зависят от направления вектора смещения s и относительной ориентации осей чувствительного элемента X, Y, Z.

Метрологические аспекты механики волновых полей

Поскольку волновые механические процессы являются проявлением реакции механизма или сооружения на энергетические воздействия, выбор метрологического параметра определяется способом или принципом достоверного преобразования диагностического параметра в измеряемый электрический сигнал: деформаций - виброметром, виброскорости - велосиметром, виброускорения - акселерометром. Если средство измерения построено на физическом преобразовании первой производной пространственного положения материальной точки объекта, ее динамика описывается тремя уравнениями связи проекций v_X1, v_Y1, v_Z1, v_X2, v_Y2, v_Z2 вектора v абсолютной скорости полюса О₂ и тремя уравнениями связи проекций w_X1, w_Y1, w_Z1, w_X2, w_Y2, w_Z2 вектора w угловой скорости соответственно на подвижные оси X₂Y₂Z₂ и на неподвижные оси X₁Y₁Z₁. При этом каждая проекция угловой скорости вращения на ось представляет угловую скорость вращения вокруг этой оси и может рассматриваться как вектор, составленный из суммы проекций угловых скоростей на соответствующие оси:

v_X2 = v_X1 cos (X2^X1) + v_Y1 cos (X2^Y1) + v_Z1 cos (X2^Z1);
v_Y2 = v_X1 cos (Y2^X1) + v_Y1 cos (Y2^Y1) + v_Z1 cos (Y2^Z1);
v_Z2 = v_X1 cos (Z2^X1) + v_Y1 cos (Z2^Y1) + v_Z1 cos (Z2^Z1);

 

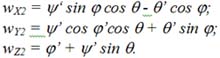
Вектор w угловой скорости и его проекции не зависят от выбора полюса, следовательно, они одни и те же для любой точки твердого тела. Аналогичным образом построено физическое преобразование как пространственного положения материальной точки, так и его второй производной.

До настоящего времени в виброметрии считалось, что воздействие "вращательных компонентов на приборы инерционного действия (ИД), предназначенные для измерения линейных компонентов вибрации, приводит к угловым искажениям и методическим погрешностям", а "чувствительность к неизмеряемым компонентам является паразитной…" Согласно общепринятой классификации виброизмерительных приборов "для взаимной компенсации неизмеряемых компонентов вибрации могут использоваться несколько дополнительных элементов. К ним относятся вращательные компоненты при измерении поступательных". При этом осторожно утверждается, что "по крайней мере в частных случаях система из нескольких приборов ИД может измерять компоненты линейных и угловых скоростей и ускорений с исключением угловых искажений".

Под влиянием воздействий происходит синтез 3D-суперпозиции спектра деформационных откликов через тензорное преобразование 3D-суперпозиции спектра напряжений (воздействий):

воздействие - упругое напряжение объекта “ ” - деформация объекта “ ”.

При отсутствии вращения физический смысл образования компонентами тензора деформаций состоит в том, что они зависят от направления вектора смещения s и от ориентации измерительных осей чувствительных элементов X, Y, Z. Измерение проводится с целью последующего анализа 3D-суперпозиции спектра напряжений, полученной путем обратного тензорного преобразования 3D-суперпозиции спектра деформаций измерительных точек (приемника):

деформация объекта - деформация датчика “ ” - упругое напряжение датчика “ ”.

Анализ физической последовательности процесса измерения деформаций позволяет сделать вывод о том, что возможен выбор системы координат, выявление связей поступательных и вращательных компонентов, нахождение механизма пересчета компонентов деформаций в соответствующие упругие напряжения. Приведенным подходом обоснована потенциальная возможность и необходимость достоверного измерения пространственных поступательно-вращательных колебательных параметров деформационных полей.

Обратное тензорное преобразование составляют идею заявленного авторами способа диагностического мониторинга механизмов и сооружений и является методологической основой инструментария для экспериментального получения достоверной метрологической информации о кинематических параметрах механических колебательных процессов в измерительных точках контурной поверхности объекта. Для практической реализации заявленного способа в задачах адекватной оценки динамической прочности и степени соответствия текущего эксплуатационного ресурса расчетным проектным показателям необходимо наличие средств достоверного мониторинга пространственных параметров механических систем.

 (Продолжение в следующем номере).