ФУНДАМЕНТАЛЬНЫЙ ПОДХОД К РЕКОНСТРУКЦИИ МЕХАНИЧЕСКИХ ПОЛЕЙ ДЛЯ ОЦЕНКИ ЭКСПЛУАТАЦИОННЫХ СВОЙСТВ ИЗДЕЛИЙ ОБОРОНПРОМА

 

Анатолий Алексеевич Сперанский,
в.н.с. РГУ нефти и газа им. И.М. Губкина
Константин Львович Захаров,
к.ф.-м.н., гл. конструктор НПП "Векторные системы"
Дмитрий Владимирович Малютин,
научный руководитель НПП "РЭМ-вибро"

Введение

Одной из причин повышения энтропии в области экотехнологической безопасности является недостаточная информативность инструментальных средств мониторинга и методов объективной оценки эксплуатационных ресурсно-прочностных показателей техносферных компонент природно-технических систем.

В области измерения волновых параметров механических систем научно-техническая революция XX века носила в большей степени экстенсивный характер и привела скорее к количественному росту научного знания, нежели к увеличению качества и глубины его понимания. Всеобщая распространенность линейных скалярных измерений, даже многомерных, привела к тому, что механический диапазон частот по сравнению с остальными физическими полями стал метрологически неинформативным. Для диагностических целей получили развитие косвенные экспериментальные способы регламентированной оценки эксплуатационного ресурса прочности, основанные на консервативных статистических моделях и сложных параметрических методах. Регулярно происходящие в мире техногенные катастрофы свидетельствуют о чрезвычайно низкой эффективности скалярного мониторинга. Механический мир скалярных измерений, малоинформативных и недостоверных, в полном смысле слова, рушится на глазах, но каким будет безопасный мир, и какие подходы в нем будут играть решающую роль - вопрос далеко не для всех, несущих бремя ответственности за безопасность среды обитания, ясный.

Информационно-технологическое отставание наиболее распространенной в инженерных приложениях виброакустической оценки энергетических показателей является следствием мировой практики несистемного измерения пространственных параметров волновых механических полей на основе ограниченных практических возможностей одноканальных скалярных метрологических средств или их несвязанных композиций. Построение амплитудно-частотных характеристик (АЧХ) без учета вращательной составляющей полных пространственных колебаний и важнейшего временного параметра - фазы колебаний, лишает достоверности спектральные измерения виброакустических полей. При этом повышается риск принятия неправильных решений, значительно искажаются оценки ресурса эксплуатационной прочности силовых агрегатов и сооружений, снижается объективность гидроакустического мониторинга и геодинамических наблюдений, что существенно снижает техногенную безопасность в машиностроении и строительстве. Вследствие сложившейся практики, главное поле среды обитания человека - частотный диапазон механических колебаний от 0 до 20 кГц, в котором реализуется фундаментальное свойство материальных объектов окружающего мира - прочность, наименее метрологически освоено. В результате общество, наделенное интеллектом и будучи цивилизованным, не чувствует себя в безопасности и все более уязвимо от сил непознанной стихии разрушений. Вместе с тем, приходит понимание того, что укоренившаяся привычка полагаться на "авось" благодаря непомерно завышенным запасам конструкционной прочности не эффективна ни в социально-экономическом, ни в энергетическом, ни в экологическом смысле. Приходит понимание того, что для обеспечения стабильности техногенного мира и безопасности среды обитания нужна концепция достижения указанных целевых функций - интеллектуальный прорыв и новое, адекватное природе, понимание сущности глобальной техногенной безопасности, фундаментальное и универсальное для всех волновых механических полей.

Метрологически противостоящие косвенным скалярным измерениям векторно-фазовые методы волновой виброакустической метрологии, достаточно глубоко обоснованные теоретически, до настоящего времени практически были недоступны. Помимо традиционного консерватизма мирового метрологического сообщества, к фактически сложившемуся положению были и объективные причины. К главным из них следует отнести технологическое отставание в области создания: а) средств достоверного мониторинга пространственных параметров механических систем; б) программно-аппаратных средств сбора, обработки и визуализации параметров деформационных полей; и в) методологии многомерной реконструкции динамических контурных характеристик ресурса прочности машин и сооружений, а также идентификационных образов сплошных физических сред.

Инновационное применение векторно-фазовых методов может быть реализовано только на основе фундаментальных законов и принципов механики.

 

Современные основы рациональной механики

Механике принадлежит выдающаяся роль в развитии современной техники, однако в минувшем столетии эта прикладная наука испытала и серьезные затруднения. Неспособность удовлетворительно описать целый ряд явлений микромира привел к длительному кризису застоя. В конце прошлого века кризис преодолен, механика динамично развивается и расширяет сферу своего влияния.

В основе всей рациональной механики, имеющей целью изучение законов Природы, управляющих поведением реальных объектов, лежит идея об объективном, т.е. не зависящем от нашего воображения, существовании реального мира. В современных физических теориях встречаются утверждения, находящиеся в резком противоречии с принципом материальной объективности, однако отказ от него равносилен отказу от признания существования объективных закономерностей природных явлений. В рациональной механике любое нарушение принципа материальной объективности рассматривается как грубейшая ошибка и считается совершенно недопустимым. Хотя сам термин "принцип материальной объективности" возник в механике всего несколько десятилетий тому назад, но на интуитивном уровне этот принцип используется с древних времен. Разумеется, что в механике допускается использование необъективных характеристик, но только весьма специальным образом, чтобы не потерять отражение физическим законом объективной реальности и достоверности.

Главное изменение в современной рациональной механике связано с введением спинорных движений и переходом на фундамент эйлеровой механики, являющейся мощным развитием ньютоновой механики. Леонард Эйлер первым установил, что ньютонова механика трансляционных движений, управление которыми осуществляется силами, принципиально не обладает полнотой. В природе помимо трансляционного существует еще один тип движения - спинорное, которое основано на другом типе воздействий - моментах, которые, в общем случае, не сводятся к понятию момента силы. Поэтому, помимо уравнения баланса сил, необходимо постулировать еще один закон - уравнение баланса моментов, которое и используется при выводе уравнений динамики твердого тела. Спинорные движения и новые законы динамики были введены Эйлером в 80-е годы XVIII века и опубликованы на латинском языке в “Вестнике Санкт-Петербургской академии наук”, до сих пор не переведены и долго оставались неизвестными большинству ученых. Эйлером впервые введены тензоры второго ранга (тензоры поворота и инерции твердого тела) и заложены основы механики сплошных сред, начало чему дали исследования по гидромеханике и теории стержней. Исторически тензорное исчисление вводилось именно в качестве языка, отражающего интуитивные образы. В огромной степени это объясняется тем, что Л. Эйлер обладал совершенно феноменальной интуитивной способностью непосредственного визуального восприятия вводимых им представлений, понятий и образов.

Последователем Л. Эйлера стал Жозеф Лагранж, введя фундаментальное понятие о тензоре малых деформаций. Однако заблуждение в том, что уравнения баланса моментов можно доказать в рамках ньютоновской механики, задержало развитие механики, по меньшей мере, на столетие и вызвало глубокие негативные последствия в современной теоретической физике. Разработка Огюстеном Луи Коши линейной теории упругости на основе тензорных представлений механики упругого континуума (тензоры напряжений, деформаций и упругости) определила дальнейший прогресс в построении механики сплошных сред (МСС). Два фундаментальных закона динамики Эйлера и два начала термодинамики составили каркас для построения современной механики. Однако, для практических приложений механики в виде моделей систем необходимы дополнительные определяющие уравнения, устанавливающие связи между основными переменными, входящими в фундаментальные законы. Характерным примером определяющего уравнения в механике является обобщенный закон Гука. Долго считалось, что построение определяющих уравнений является неустранимым звеном и задачей экспериментальной механики. Но как показало время, это теоретическая проблема, которая принципиально не может быть решена методами экспериментальной механики. Строгая теория определяющих уравнений, отражая глубину и мощь эйлеровой механики, была полностью осознана и получила законченный вид только во второй половине XX века. Объяснение преимущественного внимания ньютоновой механике кроется в том, что даже её возможности столь велики, что позволяют решать огромное множество важных теоретических и прикладных задач. А её ограниченность существенно проявилось только при описании явлений микромира.

Мысль о необходимости введения спинорных движений приходила в голову многим ученым, особенно в связи с попытками построить теорию электромагнетизма. Идея ясно выражена у Дж. Максвелла, Мак-Келлога, лорда Кельвина, Х. Лоренца, П. Дюгема, Э. и Ф. Коссеры и др., что заложило начало теории микрополярных сред, частицы которых обладают как трансляционными, так и вращательными степенями свободы. Тем не менее, и этот труд оказался невостребованным учеными того времени. Трехмерные теории микрополярных сред начали интенсивно развиваться только в последние сорок лет, когда учет независимых вращательных степеней свободы оказался необходимым в теории жидких кристаллов и теории ферромагнитных материалов.

Фундаментальные законы и принципы рациональной механики в совокупности с обобщенными законами прочности могут стать основой инновационного подхода к прямым методам оценки и реконструкции эксплуатационного ресурса механических систем.

Подходы к реконструкции свойств и образов объектов механических систем

1. Информационный подход в задачах обеспечения техногенной безопасности

Озабоченность общества состоянием техногенной безопасности среды обитания наиболее заметна в сфере технического регулирования.

В первую очередь, это относится к проектной документации новых и реконструируемых объектов. Важнейшим фактором гарантированной безопасности является не изменение нормативов в сторону их ужесточения, как это подчас декларируется, а повышение достоверности метрологических технологий.

Во-вторых, в процессе производства или строительства необходимо избежать отклонений от проекта, снижающих качество. Это задача технического надзора заказчика, которая может быть решена профессионально только с привлечением эффективного методического и программно-аппаратного метрологического инструментария.

Третьим, самым главным и массовым, в смысле общественной безопасности, уровнем является непрерывный мониторинг (эксплуатационная экспертиза) объектов путем технической диагностики на основе методов неразрушающего контроля и анализа с целью достоверного определения степени опасности - изношенности и "текущего состояния" остаточного эксплуатационного ресурса.

Все три системных уровня безопасности эффективны только при условии информационного подхода к достоверной оценке параметров эксплуатационного ресурса агрегатов и конструкций. Именно научное сопровождение может обеспечить эффективное применение инновационных технологий безопасности в реальной жизни.

2. Системный подход в задачах мониторинга среды обитания

Поскольку пространственные волновые механические поля являются системо-образующей основой среды жизнедеятельности человека, остановимся более подробно на информационно-методологических аспектах отображения полевых диагностических параметров.

Наиболее существенной характеристикой системы является структура, определяемая количеством составляющих её элементов и их взаимоотношением.

Определение структуры подтверждает необходимость, помимо амплитуды, частоты и их взаимоотношений, введения третьего компонента - временной характеристики (сдвига фаз) волновых колебательных процессов, как дополнительной характеристики, существо которой и определяет всеобщее свойство механических систем, целевые критерии достоверности измерений и общие волновые закономерности деформационных полей. Векторно-фазовые характеристики снижают неопределенность и недостоверность скалярных измерений, повышают метрологический уровень, упорядоченность и прогрессивное развитие негэнтропийного потенциала систем. Достоверное знание, как информационный акт, получает свою завершённость тогда, когда потенциальные энтропийно-негэнтропийные модели реализуются в виде объективной (адекватной) оценки с вероятностью, близкой к единице, в актуальном пространстве времени. В силу фундаментальности принципов, универсальности критериев и существенности метрологических свойств, векторное представление волновых виброакустических полей следует считать обобщенной негэнтропией (ОНГ) или связанной информацией. Единство энтропии-негэнтропии составляет основу информационного подхода формируемого современной наукой миропонимания. Высказано предположение о том, что связанная форма информации вместе с массово-энергетическими свойствами волновых деформационных полей механических систем образует единое фундаментальное информационное поле среды обитания.

Можно отметить существование признаков системной дифференциации элементов механических полей как системы - в качестве первичных элементов структуры традиционно используются спектр амплитуд и частот. Укоренившаяся практика диагностики на основе АЧХ и модального анализа передаточных функций систем, по существу, сводится к оценке текущих эксплуатационных состояний путем применения сложных статистических моделей по двум параметрам "дрожания" - амплитуде и частоте. Эти элементы являются эмоциональными, внешними показателями системы, которые отражают понимание усредненных спроецированных определенным (скалярным) образом пространственных процессов. Отсутствие векторно-фазовых параметров среди элементов структуры волновых деформационных полей приводит к неполному описанию систем и их превращений, недостоверности измерений и, как следствие, недостижению целевой функции - безопасному функционированию технических систем. В то же время, внешняя среда (энтропия) и система (негэнтропия) представляют собой природное закономерное единство, находящееся в постоянном информационном взаимодействии.

3. Влияние фазовых сдвигов на суперпозицию колебаний волновых полей

Всеобщий колебательный характер физических процессов в среде обитания человека определяет исключительную важность задачи достоверного измерения параметров волновых полей механического диапазона частот. Эту экспериментальную область знаний обеспечивают взаимосвязанные измерительные, испытательные и наладочные технологии: виброметрия, акустические измерения, сейсмометрия, динамометрия, тензометрия, тахометрия, динамическая наладка (балансировка), дефектоскопия, диагностика, а также регистрация, реконструкция, визуализация и другие технологии компьютерной обработки сигналов. Теория виброакустической метрологии охватывает принципы измерения и методы теории колебаний.

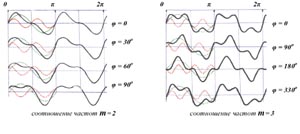
Для достоверного измерения параметров колебаний, прежде всего, требуется понимание механизма их образования. В области гармонических колебаний каждая измерительная точка объекта или среды изучения подвержена одновременному воздействию множества источников (причин, полей) подобных колебаний. Естественно, чувствительные элементы метрологических средств испытывают на себе влияние совокупности этого множества переменных пространственных воздействий (напряжений), образующих общее переменное волновое поле в качестве результирующего изменения смещений, либо деформаций, либо давления, либо суммарного тока и т.д., в зависимости от физических свойств среды, в которой происходят колебания и производится их измерение. Суперпозиция колебаний измерительной точки существенно зависит от соотношения частот m, фаз j и амплитуд слагаемых колебаний.

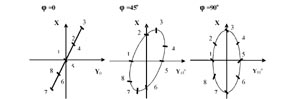
В случае двух ортогонально направленных гармонических воздействий X и Y одинаковой частоты суперпозиция колебаний представляет собой стационарный плоский эллиптический пространственно-временной годограф GXY суммарного вектора колебаний измерительной точки. Соотношение максимумов компонент определяет угол наклона годографа или его осей относительно осей координат X и Y. Относительный сдвиг фаз j между воздействиями X и Y при неравенстве максимумов деформаций, в общем случае, превращает годограф в плоский эллипс с направлением большой оси в сторону большего воздействия.

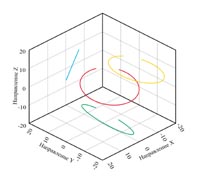
В случае трех ортогонально направленных связанных гармонических воздействий, являющихся компонентами вектора, плоскость эллипса занимает пространственное положение в соответствии с соотношением его компонент.

В общем случае произвольно расположенных воздействий суперпозиция гармонических колебаний имеет более сложный пространственный характер.

Из фазово-частотно-временного рассмотрения элементарных суммарных колебательных процессов следует, что пространственно-временные параметры результирующего годографа самым существенным образом зависят от разницы фаз составляющих суперпозицию колебаний.

4. Тензорный подход к описанию физических закономерностей сплошных сред

Фундаментальной научной основой всех механических систем является механика сплошных сред (МСС), основными постулатами которой являются концепция сплошности и принцип суперпозиции, имеющие важнейшее значение для понимания собственно физической природы прочности. Любая материальная точка объекта (твердого тела) колеблется по траектории, мгновенные координаты которой суть суммарное гармоническое колебание совокупности (множества, спектры) мгновенных значений слагаемых.

Математическим аппаратом, отражающим физические закономерности МСС, является тензорное преобразование. Тензор Т реализует связанный образ свойств, существенно отличающихся в направлении каждой из осей принятой системы координат. Тензорное представление свойств сплошных сред лишает правомерности досужие утверждения о "достоверности скалярных измерений проекции вектора колебаний". Применительно к механическим системам, изучать пространственные свойства волновых полей по измерениям произвольной совокупности несвязанных скалярных компонент математически некорректно.

5. Рациональный подход и отображение спинорных параметров

Новейшие представления о МСС основаны на том, что в физическом пространстве, т.е. в данной системе отсчета, можно наблюдать и фиксировать два принципиально различных типа движения тел. Первый тип движения характеризует перенос (трансляцию) тела в пространстве, давно изучен и легко воспринимается нашей интуицией. Второй тип движения характеризует изменение ориентации тела в пространстве и называется спинорным. Обычно такое движение тела называют вращательным, но последний термин часто применяется и при описании трансляционного движения, например, вращения Земли вокруг Солнца. Для описания спинорного движения введено понятие спин-вектора, которое также является элементом нашего интуитивного мышления. Формально для спин-вектора в пространстве вокруг оси в ортогональной плоскости вводится изображение круговой стрелки, показывающей направление вращения. Длина круговой стрелки называется модулем (длиной) спин-вектора и указывает величину вращения или поворота в трехмерном физическом пространстве. Полное движение является комбинацией трансляционного и спинорного движений.

Соответственно двум типам движения в физическом пространстве действуют два различных типа векторов. Прямые или полярные векторы задаются направлением в физическом (трехмерном) пространстве и вещественным числом (скаляром), называемым длиной или модулем вектора. Наиболее естественной интерпретацией прямых векторов является трансляция, т.е. перенос в физическом пространстве. Например, вектор силы (прямой вектор) нельзя интерпретировать как перенос в пространстве, но сила, действующая на свободное тело, вызовет его перенос в пространстве, хотя и не обязательно только перенос. Для того, чтобы тело перемещалось без вращения, необходимо выполнить определенные условия. Аналогично, вращающий момент (спин-вектор), приложенный к телу, стремится вызвать поворот этого тела. Однако работать с двумя множествами элементов различной природы неудобно. Тем более, что спин-векторам можно взаимно однозначно сопоставить прямые векторы, если ввести дополнительное соглашение об ориентации системы отсчета: а) направленный отрезок (прямой вектор) называется полярным вектором, если при замене ориентации системы отсчета на противоположную, упомянутый направленный отрезок не меняется; и б) направленный отрезок (псевдопрямой вектор) называетя аксиальным вектором, если при замене ориентации системы отсчета на противоположную упомянутый направленный отрезок меняет свое направление на противоположное, сохраняя свою длину. За аксиальными векторами всегда стоят спин-векторы, т.е. вращения в физическом пространстве. Это различие никак не связано с выбором системы координат в заданной системе отсчета. Поэтому с физической точки зрения различие между полярными и аксиальными векторами существенно и неустранимо. Целесообразно вектор полного движения в произвольной точке любого механического объекта, связывающий информацию полярного и аксиального векторов, называть бивектор. Огромное прикладное значение для реконструкции прочностных свойств имеет потенциальная возможность измерения не только параметров полного движения, но и механизм разделения комбинации на трансляционное и спинорное движения.

Характеристики спинорного движения тела - тензор и вектор поворота, могут изучаться как вполне самостоятельные объекты, не связанные с абсолютно твердым телом.

(Продолжение в следующем номере).