ТУРБУЛЕНТНОСТЬ РИМАНА-МАХА

Юрий Михайлович Кочетков, д.т.н.

Турбулентность при сверхзвуковых режимах течения представляет особый интерес. Течение вблизи движущихся в атмосфере объектов: сверхзвуковых самолетов, ракет, крылатых ракет, спускаемых аппаратов всегда сопровождается возникновением скачков уплотнения. Известны скачки уплотнения различных типов: прямые, косые, мостообразные, -образные и др. Характерной особенностью скачков уплотнения является то, что их поперечный размер весьма тонок и соизмерим с длиной свободного пробега, а термогазодинамические параметры внутри них изменяются очень сильно.

Георг Фридрих Бернгард Риман (17.09.1826 - 20.07.1866)	Эрнст Мах (18.02.1838 - 19.02.1916)

Впервые скачки уплотнения теоретически предсказал великий математик и физик Бернгард Риман. Решая задачу о распространении плоских волн конечной амплитуды, он на кончике пера сделал гениальное открытие явления разрыва течения при определенных условиях и состоянии газовой среды. Подходя к вопросу как математик, Риман скромно принижал уровень своего физического открытия, ссылаясь лишь на важность математических способов интегрирования дифференциальных уравнений газодинамики. При этом для интегрирования и доказательств полученных им новых положений он использовал новое понятие - инвариант Римана. В своих работах он не надеялся на экспериментальное подтверждение полученных им результатов, говоря при этом, что "сравнение с опытом в настоящее время едва ли возможно".

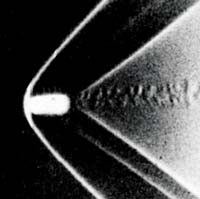
Открытие Римана просуществовало на бумаге почти сорок лет. Только в 1888 г. знаменитый аэродинамик и философ Эрнст Мах подтвердил теоретические предсказания Римана. Мах, изучая аэродинамические процессы, сопровождающие сверхзвуковой полет тел (артиллерийских снарядов, пуль и др.), открыл и исследовал специфический волновой процесс, впоследствии получивший название ударной волны. В этой области газовой динамики именем Маха назван ряд величин и понятий, широко используемых в инженерной деятельности: число Маха, конус Маха, угол Маха, линия Маха, волна Маха и др. В процессе экспериментальных исследований ему удалось зафиксировать при помощи фотографии полет латунной пули. Эта фотография в то время была революционной по существу и по форме. Она показала новый уровень исследований в физике газа и плазмы и открыла целое направление сверхзвуковой практической плазмогазодинамики. Формально она также демонстрировала новый метод теневой фотографии сверхзвуковых потоков с разными плотностями. Многие результаты и закономерности в дальнейшем были получены при помощи этого метода. В настоящее время этот и другие методы на его основе являются наглядными и весьма продуктивными с точки зрения определения количественных взаимосвязей. Они широко используются в экспериментах и испытаниях установок, работающих на сверх- и гиперзвуковых потоках газа и плазмы. При помощи интерферометра Маха-Цандера Махом была исследована интенсивность ударной волны.

Исследования, проведенные Риманом и Махом, являются основополагающими в теоретической газовой динамике сверхзвуковых и гиперзвуковых потоков, а понятие скачка уплотнения - ключевым понятием теории этих дисциплин.

Традиционным способом описания скачка уплотнения является его представление в виде разрыва газового потока при достижении критических условий. При этом в литературе приводят для его характеристики несколько свойств, установленных эмпирическим путем и строго справедливых для идеального газа.

1. Увеличение плотности и давления потока за скачком уплотнения происходит весьма круто (скачкообразно). При этом постоянное увеличение давления за скачком в отличие от обычного адиабатического (изоэнтропического) процесса не приводит постоянно к увеличению его плотности. Относительная плотность в соответствии с адиабатой Гюгонио стремится к своему предельному значению (k+1)/(k-1), где k - показатель адиабаты Пуассона.

2. При переходе через скачок также круто увеличивается энтропия (S), что приводит к локальной потере полного давления. При этом коэффициент, учитывающий волновое сопротивление (потери полного давления в прямом скачке), уменьшается с возрастанием энтропии.

3. Уменьшение скорости потока при прохождении через прямой скачок уплотнения подчиняется соотношению Прандтля.
При этом значение коэффициента скорости после скачка обратно пропорционально значению до скачка уплотнения. Прохождение через прямой скачок переводит сверхзвуковой поток в дозвуковой.

Течение реального газа при наличии скачков уплотнения представленными соотношениями может быть описано в определенной мере приближенно. Для их точного описания необходимо учитывать так называемые вязкостные эффекты. В эти эффекты включаются, кроме самой вязкости, теплопроводность, релаксация, различные типы диффузии и необратимые химические реакции в случае плазмы. Все указанные эффекты являются диссипативными в том смысле, что они вызывают возрастание энтропии. При рассмотрении этих эффектов снимается вопрос о так называемом скачке уплотнения. Параметры в реальном газе изменяются не в бесконечно малой области, а в совершенно конечном пространстве, ограниченном некоторой фиксированной шириной. Экспериментально-расчетным путем было установлено, что эта ширина составляет несколько средних длин свободного пробега молекул в газе и зависит от степени его разреженности.

Другой термин, употребляемый в теории скачков уплотнения, - ударная волна. Этот термин больше подходит для подобных течений реальных газов, так как предполагает наличие больших, но конечных градиентов практически всех параметров. В этом случае говорят о ширине ударной волны, не уточняя, совпадает ли она с длиной волны, образующейся в этой области. Понятие ударной волны предполагает не только изменение абсолютных параметров до и после волны, но и характеризует динамику ее распространения. Появляется понятие градиента плотности газа dr/dx, который принимает свое максимальное значение внутри интервала между установившимися значениями до и после ударной волны. Пик градиента плотности реализуется в области критических скоростей звука (a_кр), а сам переход из области сверхзвукового течения в дозвуковое в прямой ударной волне сопровождается плавным замедлением скорости в сверхзвуковой области до значения a_кр и в дозвуковой области до соответствующего значения. Аналогичная ситуация происходит в косой ударной волне. При этом касательная составляющая скорости не меняется, так как сверхзвуковой поток просто скользит в направлении линии ударной волны, а нормальная составляющая движения ведет себя так же, как скорость в прямой ударной волне.

Таким образом, ключевым моментом течений внутри ударных волн является переход через критическую скорость звука. В отличие от течений в соплах, эти течения происходят с положительными градиентами давления (dp/dx > 0) и отрицательным градиентом скорости газового потока (dw/dx < 0).

В соответствии с теми же выкладками отмечаем, что величина прироста энтропии в ударной волне пропорциональна величине положительного градиента давления dp/dx. Максимальная его величина реализуется в точке перегиба кривой р(х). Максимальный наклон этой кривой соответствует максимальному числу Рейнольдса в волне, что указывает на то, что в этой области реализуется максимальная турбулентность. Как было отмечено в предыдущей работе ("Двигатель" № 4 (46) - 2006), максимальное число Рейнольдса реализуется при условии критических параметров потока
a = a_кр.

В статье, опубликованной в журнале "Двигатель" № 1 (49) - 2007, было введено семь устойчивых конфигураций турбулентного потока. Последовательность их такая: ламинарное течение, волны Толмина-Шлихтинга, градиентные волны Кельвина-Гельмгольца, вихри Тейлора - Гертлера, закрученные жгуты, течение при критических параметрах потока и отдельно выделялись волны Маха. Было доказано, что максимальная турбулентность реализуется при критических параметрах потока (М= 1). В этой области течение становится вновь ламинарным, так как скорость течения равна тепловой скорости молекул, а ее суммарное направление соответствует условиям детерминированного хаоса. При последующем движении сверхзвукового потока течение всегда остается ламинарным. Исключением являются зоны больших положительных градиентов в области возникновения ударных волн. В общем случае эти зоны являются зонами турбулентности, и внутри них могли бы реализовываться все названные устойчивые состояния. Однако в силу малости ширины ударной волны, а точнее еще большей малости ее дозвуковой части, большинство составляющих турбулентного движения будут отсутствовать. Характерные для макродвижений вращение и кручение потока не могут реализовываться на ширине нескольких длин свободного пробега молекул. Основными видами турбулентного движения остаются поступательное и волновое. Возможна их комбинация в виде биения.

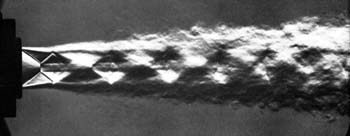
Специальным случаем турбулентного течения является течение в сверхзвуковом сопле с ударными волнами и сверхзвуковые струйные течения. Здесь области положительных градиентов давления взаимодействуют с областями отрицательных градиентов, формирующимися при раскрытии сопел и расширении струй. На общем фоне ускоряющегося потока периодически возникающие скачки уплотнения образуют картину чередующихся ламинарных и турбулентных областей. При этом нарастающая турбулентность срабатывается в волнах Маха. Струя ограничена системой скачков уплотнения, выстроенных в строгом соответствии с классическими формами. Струи из всех шести двигателей имеют полностью повторяющиеся формы, что говорит о высокой устойчивости течения.

Представленные в работе результаты дополняют общую картину возможных турбулентных течений и уточняют представление о турбулентности в сверхзвуковых потоках.

[Напоминаем, что Интернет-вариант статьи сильно сокращен. Ред.]