ТУРБУЛЕНТНОСТЬ СЛОЖНЫХ КАНАЛОВ

Юрий Михайлович Кочетков, д.т.н.

Анализ различных видов турбулентности в сложных каналах подтвердил справедливость следующих утверждений: турбулентность представляет собой систему устойчивых форм течения; турбулентность - это комбинация четырех видов простых течений (поступательного, волнового, вращательного и торсионного); максимальная турбулентность (ламинарность) реализуется в критическом сечении, а в сверхзвуковой части турбулентность отсутствует.

Трехмерное течение жидкости, газа и плазмы внутри камер, сопел, воздухозаборников и других проточных трактах, ограниченных твердыми стенками с поверхностями сложных форм, как правило, является турбулентным. В общем случае в любом, даже в самом простом канале, имеющем высокую степень симметрии (журнал "Двигатель" № 6 (42) - 2005), течение может быть достаточно сложным и зависеть во многом от режима, определяющего комбинацию независимых видов течения. Наличие поворотов, вращений, колебаний стенки и совместное воздействие этих факторов на рабочее тело приводит дополнительно к усложнению структуры потоков и возникновению новых устойчивых форм.

В каналах можно условно выделить три независимых вида течений: течения в осесимметричных каналах; в несимметричных каналах; в осесимметричных каналах с несимметричными условиями на входе.

Указанные виды течений могут комбинироваться. Например, повернутое относительно оси камеры сгорания эллиптическое сверхзвуковое сопло с косым срезом совмещает в себе осесимметричное течение вдоль цилиндрической камеры, поворот в сверхзвуковую часть сопла, течение внутри сопла с эллиптическим проходным сечением и истечение через косой срез с последующим резким поворотом потока. Аналогичными течениями являются течения в турбинах и насосах ЖРД, где процесс усложняется вращением.
Сложные формы каналов могут приводить к самым разнообразным ситуациям и порождать бесконечное многообразие различных структур потоков. Комбинации трех перечисленных видов течений могут приводить к возникновению вторичных, третичных и многоразветвленных течений. При их математическом описании приходится сталкиваться с все более сложными способами задания граничных условий, адекватно описывающих условия течения.

Многие течения в сложных каналах в настоящее время не удается предсказать аналитически или расчетным путем. Для их описания используют экспериментальный подход, который, к сожалению, также не всегда позволяет получить желаемый результат. В таких случаях используют эспериментально-расчетные методы моделирования течений в сложных каналах.

Течение в осесимметричном коническом сопле

Наиболее характерным примером является течение в сверхзвуковом разгорающемся осесимметричном коническом сопле. Изучение структуры такого течения проводилось на модельной твердотопливной установке с соплом из фторопласта. Были исследованы сопла с различными углами раскрытия сверхзвуковой части. Эксперименты проводились с использованием различных составов твердого топлива, при различных давлениях в камере сгорания и различном процентном содержании конденсированных продуктов сгорания (Z = 0…0,4). В результате исследований было установлено, что разгар в закритической области происходит в устойчивом газодинамическом режиме. В месте перехода от неразгорающегося вкладыша критического сечения к разгорающемуся фторопластовому конусу возникала так называемая "закритическая яма", в которой формировалась зона дозвукового течения с образованием вихрей Тейлора-Гертлера. Вихревая структура фиксировалась методом горячей визуализации. Со временем эта структура не изменялась, количество вихрей сохранялось, а размеры их увеличивались пропорционально времени разгара.

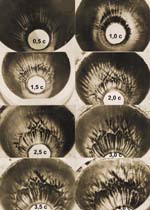
Амплитуда вихрей функционально связана также с максимальной глубиной "ямы". Экспериментальная зависимость величины максимального уноса, полученная для конусов с различными наклонами образующих, выглядит как однозначно зависимая от угла входа в сверхзвуковую часть сопла.

При достаточно сильных разгарах ниже по потоку были зафиксированы ячеистые образования, равномерно расположенные по окружности в шахматном порядке. Это следы кручения потока. Они подробно описаны в журнале "Двигатель" № 4 (40) - 2005.

Турбулентность в призматическом сопле

Призматическое или прямоугольное сопло имеет в поперечном сечении либо прямоугольник, либо квадрат. При этом угол наклона одной пары противоположных плоскостей равен нулю. Если высота прямоугольника намного меньше ширины, то сопло вырождается в плоское щелевое.

Особенность течения в призматическом сопле состоит в том, что расширение потока вдоль смежных плоскостей различное и больше там, где угол наклона их к оси больше. Это должно было бы приводить к аксиальным течениям. Но поскольку ("Двигатель" № 4 (46) - 2006) в сверхзвуковом потоке турбулентность отсутствует, то в таком сопле формируется пространственная система скачков. Вблизи стенок, по месту разгара сопла, образуются дозвуковые зоны. Локальные давления в этих зонах соответствуют степеням расширения вдоль каждой из образующих плоскостей, где формируются соответствующие аксиальные течения.

Эксперименты, проведенные на призматических соплах из фторопласта показали, что на гранях призм образовывались вихри Тейлора-Гертлера. Величины амплитуд этих вихрей были обратно пропорциональны величинам углов наклона плоскостей и подчинялись зависимостям для конического сопла. В соответствии с этими зависимостями амплитуды вихрей исследованных сопел различались друг от друга примерно на 20 %.

В процессе работы модельного двигателя в области пересечения плоскостей, на ребрах призмы, образовался более крупный единичный вихрь размером в 2,5…3 раза превышающий любой из вихрей на гранях сопла. Очевидно, что парность этого вихря обеспечивается вихревыми течениями в ядре потока на некотором удалении от стенки.

Турбулентное течение в эллиптических соплах

Аналогичное течение было получено в экспериментах на эллиптическом сопле. В отличие от предыдущего случая призматического сопла, углового вихря на эллиптическом сопле не было. При этом размеры вихрей Тейлора-Гертлера изменялись обратно пропорционально углу наклона образующих. Они были крупнее вдоль малой оси эллипса и мельче вдоль большой. Анализ разгоревшихся сопел позволил установить неравномерность ячеистых отпечатков, располагающихся вниз по потоку за продольными вихрями. Вдоль образующей, лежащей в плоскости малых осей, ячейки были крупнее, а больших - мельче. Ячейки располагались в шахматном порядке со сдвигом на полпериода. Это были отпечатки противоположно вращающихся парных жгутов, образовавшихся в результате кручения потока. Анализ показал, что область кручения потока находилась в месте нулевого градиента давления.

Анализ турбулентных потоков в сегментном сопле

Сегментные сопла используются для отвода выхлопных струй вспомогательных двигателей от поверхностей корпусов и ответственных узлов на ракете. Как правило - это конические сопла с плоским срезом параллельным оси камеры. В области, где сопло "срезано" поток отклоняется относительно конической стенки.

Эксперименты показали, что за местом излома на плоскости дополнительно возникают области турбулентности Тейлора-Гертлера. Интенсивность вихрей прямо пропорциональна разности углов образующей конуса и наклона плоскости среза. Вихри в данном случае возникают после натекания сложного турбулентного вторичного потока, сформированного "закритической ямой" в недеформированной сегментом части сопла. Образовавшееся за изломом новое вихревое течение является третичным, так как получено усложнением предыдущего вторичного. Это новое течение - такое же упорядоченное, как и вторичное. Оно вихревое, а размеры вихрей Тейлора-Гертлера соизмеримы с размерами вихрей вторичного течения.

В области сопряжения конической поверхности и плоскости среза отмечаются одиночные более крупные вихри. Природа их аналогична вихрям в ребрах призматического сопла.

Течение в кососрезанном сопле

Кососрезанное сопло используется для резкого поворота сверхзвукового потока на угол до 30…40° относительно оси камеры сгорания и создания постоянной управляющей боковой силы. Эксперименты методом горячей визуализации на таких соплах показали, что наличие косого среза не оказывает никаких воздействий на турбулентную структуру предыдущего сверхзвукового течения. Все формы устойчивости потоков у стенки не претерпевают никаких изменений при переходе на короткую, длинную и срединную образующие. При этом проявляется характерное для всех сверхзвуковых течений свойство, когда обратная связь вверх по потоку отсутствует, а течение никак не реагирует на приближающиеся преграды и изменения формы стенки сопла.

Наличие косого среза не приводит к возникновению положительных градиентов давления если самая длинная часть стенки работает в расчетном режиме. В случае, если она работает в режиме перерасширения, то в этой области возникают локальные вторичные пространственные течения внутрь сопла.

Поворотное управляющее сопло (ПУС)

Турбулентное течение в поворотном управляющем сопле существенно зависит от условий на входе в сверхзвуковую часть ("Двигатель" № 2 (20) - 2002) и в зависимости от этих условий, а также от длины и формы сверхзвукового сопла, формируется структура течения на наветренной и подветренной части. Тривиальный поворот сопла относительно камеры сгорания не может служить критерием возникновения наветренной стороны в области наибольшего геометрического угла атаки. Вдоль стенки ПУС происходит перераспределение давления, которое имеет колебательный характер. На одной и той же образующей, в зависимости от условий течения, могут последовательно располагаться наветренные и подветренные зоны. При этом возникающие боковые усилия периодически меняют знак. С определенным периодом изменяются тепловые потоки, приводящие к несимметричному уносу. Газодинамическая структура двухфазного турбулентного потока также меняется и становится несимметричной. На наветренной стороне виден след несимметричного прогара стенки сопла.

Разрезное управляющее сопло (РУС)

Разрезное управляющее сопло отличается от ПУС тем, что поворот потока осуществляется в сверхзвуковой его части. Под воздействием рулевых машинок часть сопла вводится в поток, а часть из него выходит, образуя зоны наветренного и подветренного течений, формирующие результирующую эпюру сил давления и боковой силы. Возникший при повороте стенки в сторону потока положительный градиент давления приводит к образованию вихрей Тейлора-Гертлера. Аналогичная картина была получена на сегментном сопле. Образовывались третичные течения. Но вопреки ожиданию более сложной картины течения, когда высокотурбулизированный поток у стенки натекает на излом, подобный клину, и разбивается в области удара об нее, его структура наоборот упрощается и становится похожей на структуру вторичного течения. Размеры вихрей Тейлора-Гертлера по-прежнему удовлетворяют зависимостям для амплитуды, а их форма и количество со временем не изменяются.

Торсионные структуры в высотном сопле при испытании в диффузоре

При испытании высотного сопла модельного ЖРД в диффузоре были зафиксированы следы трехмерного течения на стенке, проявившиеся в виде отпечатков конденсированных продуктов сгорания углеродсодержащего топлива (сажи). Структуры были получены Н.Б. Пономаревым. Видны ячеистые образования на поверхности диффузора, расположенные в шахматном порядке со сдвигом на полпериода. Эти образования возникли в результате контакта попарно скрученных жгутов со стенкой сопла. Такое торсионное течение сформировалось после втекания продольных вихрей Тейлора-Гертлера в безградиентную область. При этом пары соседних вихрей образовали устойчивые жгуты (скрутки), выстланные на поверхности стенки. Аналогичная картина (меньшего масштаба), была описана в журнале "Двигатель" № 2 (38) - 2005.

Турбулентность при запуске сопла

В известном альбоме Милтона Ван-Дайка приведена фотография Г. Аманна, зафиксировавшая процесс запуска в сопле. Автором получена уникальная структура нестационарного момента истечения. Диск Маха, отмеченный на фотографии свидетельствует о том, что даже при нестационарных процессах турбулентные структуры не хаотичны, а строго упорядочены. Полученная фотография является доказательством того, что турбулентность в сверхзвуковом потоке отсутствует и, начиная с критики вплоть до системы скачков уплотнения, течение остается ламинарным. Внутри ламинарного течения выстраивается система волн Маха, проявляющаяся в виде тончайших характеристик. В дозвуковой области камеры и за системой скачков отмечается турбулентное течение в виде вихревых и жгутовых образований. Критическая область выделяется в виде однородного светлого пятна. Здесь реализуется максимальная турбулентность, и течение переходит в ламинарное.

Поскольку степень расширения сопла в зоне прохождения диска Маха очень высокая, скорость после скачка достаточно низкая и течение в следе также ламинарное.

Турбулентность при запуске воздухозаборника

Аналогичная картина была зафиксирована при запуске модельного воздухозаборника. В начальный момент перед воздухозаборником садится прямая ударная волна, которая по мере его заполнения деформируется и втягивается внутрь. На кромках воздухозаборника постепенно возникает система присоединенных косых скачков. Эта система постепенно развивается и скачки смыкаются, пересекаясь в центре. При достижении рабочего давления в воздухозаборнике система косых скачков устанавливается и далее не меняется.

Структура в воздухозаборнике в начальный момент времени турбулентная, так как за первоначальной ударной волной поток прошел через звук и стал в соответствии с формулой Прандтля дозвуковым. Поскольку скорость натекающего сверхзвукового потока сравнительно небольшая (число М ~ 1,5), то дозвуковая скорость получается значительной и соответствует турбулентному течению. При запуске сверхзвукового воздухозаборника течение внутри него устанавливается ламинарное. Внутри этого течения устанавливается система волн Маха. Внешнее обтекание воздухозаборника также происходит в ламинарном режиме.

Приведенные выше примеры турбулентного течения в каналах сложной формы являются наиболее показательными. Они охватывают основные положения волновой теории и подтверждают основополагающие утверждения.