ТУРБУЛЕНТНОСТЬ ЛЕОНАРДА ЭЙЛЕРА

Юрий Михайлович Кочетков, д.т.н.

15 апреля 2007 г. исполнилось 300 лет со дня рождения замечательного русского ученого, члена петербургской Академии наук Леонарда Эйлера. Великий математик и физик Леонард Эйлер оставил после себя бесценную сокровищницу трудов по вариационному исчислению, математическому анализу, обыкновенным дифференциальным уравнениям, степенным рядам, дифференциальной геометрии, теории чисел, функций комплексных переменных, теории приближенных вычислений.

Леонард Эйлер - ученый необычайной широты интересов и творческой продуктивности. Он является автором более 800 трудов, среди которых работы по небесной механике, оптике, баллистике, кораблестроению, прочности и даже теории музыки, оказавших значительное влияние на развитие науки.

Наиболее значимыми были достижения в области гидрогазодинамики и механики сплошных сред. Великий французский математик и механик Жозеф Луи Лагранж говорил: "Эйлер заложил основы гидрогазодинамики". В своем трактате "Общие принципы движения жидкостей" (1755 г.) Эйлер впервые вывел основную систему уравнений движения идеальной жидкости, положив этим начало аналитической механике сплошной среды. Гидродинамика обязана Эйлеру тем, что он расширил понятие давления на случай движущейся жидкости, а понятие скорости течения впервые начал рассматривать как отношение пройденного пути к времени. Ведь до него считалось невозможным вводить подобные величины.

Эйлеру принадлежит первый вывод уравнения неразрывности жидкости, своеобразная и ныне общепринятая формулировка теоремы об изменении количества движения применительно к жидким и газообразным средам. Ему принадлежит вывод так называемого турбинного уравнения, создание теории реактивного колеса Сегнера и многое другое.

Велика заслуга Эйлера в разъяснении вопроса о природе сопротивления жидкостей движущимся в них телам. Эйлер разъяснил сущность парадокса Даламбера, показав, что причина сопротивления лежит в несоответствии модели безотрывного обтекания тел идеальной жидкостью процессам, протекающим в реальной жидкости.

Гидрогазодинамическим наследием Леонарда Эйлера пользуются ученые всего мира. Общепризнана роль Эйлера как основоположника теоретической гидрогазодинамики, предопределившего своими исследованиями ее развитие на столетия.

В предисловии к сочинению "Механика, то есть наука о движении, изложенная аналитическим методом" Эйлер написал: "Первый и второй том я составил так, чтобы человек, имеющий достаточный опыт в анализе конечных и бесконечных, мог с поразительной легкостью все это понять и все это произведение прочесть без чьей бы то ни было помощи".

Турбулентное движение в отличие от ламинарного послойного, на первый взгляд неупорядоченное случайное движение, является сложным упорядоченным пространственным течением, имеющим волновую природу. На самом деле турбулентное течение строго детерминировано. Как говорил великий французский физик Пьер Симон Лаплас о законах природы, они "подразумевают полную предсказуемость и строгий детерминизм, а случайность - порождение несовершенства наблюдений". А раз так, то структуру турбулентности человек в конце концов выразит в виде изящных уравнений математической физики, а также в виде их конечных решений. Волновая теория базируется на уравнениях Эйлера и Навье-Стокса и предполагает, что любое пространственное течение (суть турбулентное течение) можно представить в виде разложения его на четыре независимых вида: поступательное, волновое, вихревое и закрученное. Другими словами, любую комбинацию из этих течений, или даже каждое в отдельности (кроме поступательного послойного) уже можно считать турбулентными, а так называемые пульсационность и мелкомасштабность являются лишь частными свойствами таких течений.

Записывая в общем виде векторное уравнение движения, справедливое для турбулентного течения несжимаемой жидкости

мы учитываем все виды пространственного течения в их совокупности. При этом каждый член записанного уравнения определяет тот или иной его вид.

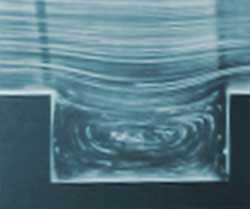Поступательное движение определяется, в основном, статическим давлением, то есть величиной gradP. В случае, если вихревое движение вообще отсутствует, то для потенциала скорости V = grad уравнение движения может быть существенно упрощено и в приближении несжимаемой жидкости записано в виде: = 0. Это случай потенциального течения жидкости.

Волновое движение можно иллюстрировать специальным классом течений с постоянной энтропией. Это течение со скоростью, равной скорости распространения малых возмущений, например, малых сжатий, или, что все равно, со скоростью звука (а₀).

В данном случае уравнение Эйлера совместно с уравнением неразрывности может быть преобразовано до волнового уравнения гиперболического типа. При этом малые возмущения скорости (u) находятся в прямой зависимости от акустической скорости газового потока.

Из уравнения Эйлера, записанного в форме Ламба-Громеки, также явно выделяется третья составляющая турбулентного течения, это - вихревое движение. Это уравнение описывает чисто вихревое течение. На основании этого уравнения доказывается очень важная для теоретической газовой динамики теорема Гельмгольца: "В движущейся под действием консервативного поля объемных сил идеальной несжимаемой жидкости вихревые линии сохраняются".

Самое сложное движение газа - кручение связывается с последним членом уравнения движения. Этот член появился в процессе вывода векторного уравнения Навье и Стоксом. Одновременно при выводе этого уравнения произошло уточнение уравнения Эйлера - его скорректировали на величину вязкого трения. Были проанализированы силы касательных напряжений, напряжений сдвига и в итоге напряжений кручения. Величина "вязкостного" члена во многих случаях является решающей в развитии структуры турбулентности, а соответственно кручение является самым высокодифференцированным элементом движения среди всех рассмотренных выше. К сожалению, исследования этого вида движения находится в самом начале. Оно требует специального изложения и поэтому, возвращаясь к теме данной статьи, рассмотрим случаи турбулентных течений, когда последний член уравнения Навье-Стокса не является существенным, а процесс турбулентного течения может с успехом быть описан векторным уравнением Леонарда Эйлера.
Очевидно, что существуют три возможности, при которых можно пренебречь силами вязкого трения и членом .

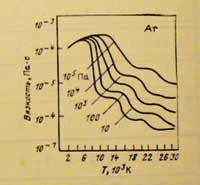
Турбулентность при . Это случай, когда пространственные течения жидкости, газа и плазмы, при которых величина динамической вязкости весьма мала по сравнению с типичными течениями газа, например, в соплах ЖРД, РДТТ или при обтекании летающих объектов воздухом. Самая низкая вязкость в классе простых газов - вязкость газообразного водорода. По сравнению с другими газами она в 2…3 раза ниже и при нормальных условиях составляет = 8,94·10-6 Па·с. Эта величина на два порядка ниже вязкости некоторых сжиженных газов и также на порядок ниже, чем вязкость плазмы воздуха при атмосферном давлении и температуре 15000 К.

Вязкость газа очень сильно увеличивается с увеличением температуры и в определенном, достаточно большом, диапазоне температур может быть описана степенной зависимостью ~ Т^m, где показатель степени m для воздуха составляет 0,76.

Интересным является то, что при определенных условиях, слабо ионизированной плазмы, состоящей из нейтральных частиц, электронов и положительно заряженных ионов, ее вязкость может существенно отличаться от нейтральных газов. Вклад ионов в вязкость становится существенным уже при малой степени ионизации, поскольку сечение обмена импульсом, происходящего при столкновениях иона с атомом и обусловленного процессом резонансной перезарядки иона на атоме, существенно превышает сечение передачи импульса при соударениях атомов. При слабой ионизации величина вязкости растет до определенного максимума, а при достижении значительной величины сечения резонансной перезарядки иона на атоме начинает резко падать. При этом зависимость вязкости от температуры становится также падающей. Видно, что значения вязкости различаются на три порядка. При этом ее резкое высокоградиентное падение вначале переходит в почти пологую зависимость от температуры. Этот факт дает возможность использования уравнений Эйлера в качестве расчетных уравнений .

Течение при V(х, у, z) = 0. При условии, когда лапласиан от вектора скорости равен нулю, расчет турбулентного течения также можно проводить с использованием уравнений Эйлера. Поскольку результатом операции лапласиан от вектора является тензор, то однозначного значения в виде константы или функции получить в общем виде невозможно. Необходимо решать уравнение Лапласа в рамках теории потенциала.

Анализ решений следует провести специально. В данном случае ограничимся конкретной зависимостью, показывающей сложность общего решения. Физическая интерпретация тензора V на сегодняшний день недостаточна и требует дальнейшего изучения.
Условие |gradP| >> | |.

Другими словами, при очень больших числах Рейнольдса уравнение Навье-Стокса можно заменить уравнением Эйлера. На практике критерий Рейнольдса не может быть равен бесконечности. Он стремится к своему предельному значению , а течение при этом достигает предельной турбулентности, то есть вновь становится ламинарным (журнал "Двигатель", № 4 (46) - 2006). Это нетрадиционное утверждение на первый взгляд может показаться шокирующим. Ведь, казалось бы, что поток, турбулизируемый всякими механизмами и преградами, градиентами и вязкостями, только запутывается, перемешивается и закручивается, а он в итоге становится высокоупорядоченным. Да, это так. Поток стремится к хаотическому, то есть тепловому движению, такому изотропному движению, когда его свойства аналогичны свойствам ламинарного течения. На практике эти свойства проявляются при течениях с малыми скоростями до момента образования волновых течений и при сверхзвуковых течениях.

Суммируя результаты сделанного анализа, точно можно сказать, что применение уравнений Леонарда Эйлера для описания турбулентных течений возможно при ламинарных и сверхзвуковых режимах. При низких значениях динамической вязкости этот диапазон расширяется. В дальнейшем, следует внимательно изучить физическую сущность тензора V - это откроет дополнительные возможности использования векторного уравнения Леонарда Эйлера, а математическая интерпретация этого факта ( V = 0) определит его точные границы.