ВИХРЕВАЯ МЕХАНИКА ПЕРЕМЕЖАЮЩИХСЯ СРЕД
(ПОСОБИЕ ДЛЯ ВСЕХ ИНТЕРЕСУЮЩИХСЯ)

Александр Григорьевич Прудников, д.т.н., ЦИАМ

(Окончание. Начало в № 6 - 2006 , № 1 -2007)

Вихревые кинетики разных иерархических уровней

 

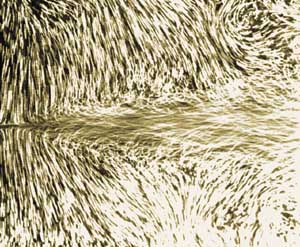Струйный вихревой слой в потоке

Используя описанные физические модели вихревых движений, можно получить аналитические решения уравнений движения потока. Это справедливо для различных масштабов как всех видов хорошо известных в газовой динамике естественных пограничных течений (СПС, ППС, струя, ближний и дальний след, псевдоскачок, концевые вихревые шнуры), так и новых искусственных пограничных течений теплогазоаэродинамических профилей: лобовых, боковых и кормовых обтекателей скоростного летательного аппарата, его силовых исполнительных устройств управления, стабилизации и тяги.В данной статье нет возможности и необходимости останавливаться на каждой задаче классического и рукотворного пограничного течения, но назрела необходимость пояснить взгляды на эти уравнения с позиций вихревой МПС.

Традиционно применяемые "точечные" нестационарные дифференциальные уравнения Навье-Стокса имеют дело со сплошной средой только в размерах самой "точки", исчисляемой сотыми долями миллиметров (размерами самых мелких турбулентных вихрей). Это слишком незначительная величина для исследования фронтов подогрева, фронтов накопления радикалов, фронтов химических реакций, негорящих и горящих "поверхностей" контактного разрыва очень малой, но конечной толщины. Решая уравнения такого уровня "сеточными методами", мы улавливаем только особенности крупномасштабного движения, определяя, впрочем, его частоты и масштабы скоростей по подсказкам физического эксперимента.

Бессистемное осреднение дифференциальных уравнений по времени дает еще меньше информационной прибавочной стоимости при избытке "шумовой информации" ввиду терпеливости и бессловесности самих уравнений. Такое суммарное тотальное временное осреднение "общим чохом" выдает результат в виде неразличимого по составу набора из жидкостей, различных присутствующих в процессе газов, движущихся многокомпонентных сред. Для ВРД в этот "фарш" добавляются, кроме воздуха, жидкого и газового горючего, еще и нагретые пристенные воздушно-горючие и в разной степени сгоревшие вихри, их "поверхности" смешения и фронты горения. С позиции статистического структурного анализа все это должно быть заменено предметно-систематизированным, условным или "своим" для каждого уровня кинетики осреднением со своей лагранжевой системой координат и структурными параметрами "черного ящика" выхода на более высокий иерархический уровень.

В термогазодинамических процессах в авиадвигателе можно усмотреть не менее пяти-шести уровней кинетик, обеспечивающих требуемую заранее точность решения и расчета: молекулярная и турбулентная кинетики со своими структурными термодинамическими и микрогазоаэродинамическими параметрами ; кинетика крупного (живого) вихря и его следа распада; статистическая кинетика ансамблей крупных вихрей разных каскадов; кинетика потенциального обтекания детерминированного (когерентного) или стохастического вихревого слоя (статистического ансамбля крупных вихрей) спутными потоками; кинетика ядер спутных потоков; кинетика суммарного движения в каналах сжатия, энерговыделения и расширения.

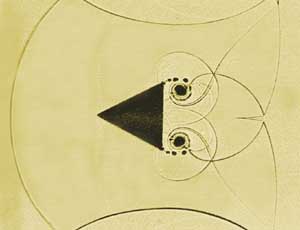
Сверхзвуковое обтекание клина

Резюмируя сказанное, можно сделать такие выводы: корреляционные моменты есть результат хаотического суммарного временного осреднения перемежающихся и перемежаемых потоков и их произвольного нефизического разбиения на "средние" и "турбулентные" пульсации; разбиение и систематизация по реальным разнородностям потоков избавляет нас от проблем, которые мы сами создаем, чтобы их преодолевать; при любом пасьянсе "полуэмпирических констант": надуманных, но согласованных с экспериментом и с любой половиной потоков (продольных или поперечных) для всех известных осредненных уравнений движения (Рейнольдса, Ротта, или современных "высокомоментных") получаем только один банально очевидный результат: пригодность (действенность) дифференциальных уравнений движения, при котором (при любом способе их осреднения и разбиения квазилинейного или перемежаемого) стотридцатилетний стаж пасьянсовой "полуэмпирической игры" с уравнениями движения хаотического (временного) суммарного осреднения является серьезным основанием сделать эту игру бессмертной, подобно шахматам, картам, нардам и т.п.
Вихревая теплоаэромеханика пограничных течений авиадвигателя и его летательного аппарата, как часть механики перемежаемых и перемещающихся взаимодействующих сред, описывается достаточно точно 24-мерной системой лагранжево-эйлеровых уравнений детерминированных и стохастических движений счетного множества разнородных сред с дискретным или непрерывным статистическим распределением своих размеров.

Известные модели классических кинетик движения: молекулярного (Максвелла-Больцмана); сплошного (непрерывного) идеального и вязкого (Эйлера, Навье-Стокса); пограничного (Кармана-Прандтля); локально-турбулентного (Рейнольдса-Ричарсона-Колмогорова-Обухова) и возможные новые модели движений крупных вихрей можно рассматривать как "черные ящики" с постоянными по объему "ящика" известными структурными параметрами, или параметрами выхода на более высокий иерархический уровень кинетики. Для молекулярной кинетики таковыми являются известные локальные значения термодинамических параметров (массы, импульса, энергии) и локальных скоростей их градиентного обмена. Для локальной турбулентности выходными параметрами являются известные локальные значения скоростей турбулентных пульсаций, скорости их затухания, скорости фронтального микротурбулентного горения и т.п. Для кинетики крупного вихря - это известные средние по объему вихря термодинамические параметры (завихренность, температура, скорости поступательного движения, роста, инжекции и др.), определяемые решениями без эмпирических констант "парциальных" (условно средних) уравнений движения ядра единичного крупного "вихревого клубка" постоянной завихренности. Для статистической кинетики вихревого слоя, состоящего из статистического ансамбля живых крупных вихрей и их следов распада, - это известные размеры все более крупных вихрей, образующихся спариванием (перингом) бесконечного множества каскадов и геометрические параметры вихревого слоя, определяемые системой дифференциальных уравнений вероятностей появления этих каскадов, включая нулевую вероятность ПТР.

Крупные и турбулентные вихри имеют независимые, соответственно, обратимый и необратимый источники энергии, описываемые достаточно точно нульмерными балансными условиями сохранения энергии.

Двух- трехчленные приближения единых формул классических профилей теплогазоаэродинамических параметров вдоль и поперек суммарных пограничных течений более точно описывают экспериментальные профили, чем разновидовые известные "диффузионные" "логарифмические" и степенные аппроксимации свободных, пристенных "следовых" и струйных погранслоев.

Разбиение неоднородного и неизотропного поля разнозначных газоаэродинамических параметров на поле средних значений и поле слабых (линейных) мелкомасштабных "турбулентных" пульсаций для реальной вихревой макромеханики перемежаемых, перемежающихся и реагирующих сред некорректно, так как дает ошибку до 45 % для при одном только и выносе плотности из-под знака осреднения тензора и создает непреодолимые (надуманные) проблемы с определением корреляционных моментов (при условном осреднении по однородным объемам разных сред таких проблем не возникает).