ТУРБУЛЕНТНОСТЬ СЛОЖНЫХ ФОРМ

Юрий Кочетков, д. т. н.

Нас окружает великое множество видов течений жидкостей и газов. Все эти виды условно укладываются в две большие группы: "ламинарные течения", когда каждая частица жидкости движется параллельно основному направлению потока, "течения турбулентные", когда поток представляется огромным количеством отдельных самостоятельных вихрей. Вся газовая динамика, теория полета, гидро- и аэродинамика в конечном счете - лишь попытка понять механику образования этих видов течений и взаимодействия их с различными телами, поверхностями и каналами, а также найти методы математического расчета этих процессов.

Обратим внимание именно к последнему из упомянутых течений: к турбулентному. Все многообразие видов турбулентного течения, можно разложить на несколько элементарных, взаимодействие которых даст картину любого, даже самого замысловатого. Хаотическим оно кажется лишь потому, что наше зрение не позволяет зафиксировать быстротекущие процессы и мелкомасштабные структуры. К сожалению, это не всегда удается даже при использовании высокоточной тепловой, оптической и лазерной техники. Часто это происходит из-за неумения правильно поставить эксперимент.

О. Рейнольдс первым предложил для визуализации вихрей в жидкости использовать окрашенные струйки. Первыми применил фотографию при исследовании ламинарных течений английский гидродинамик Хеле-Шоу, а турбулентных - немецкий ученый Ф. Альборн. Но идею о фотографировании струй на 15 лет раньше выдвинул русский писатель М.Е. Салтыков-Щедрин в "Современной идиллии".

Для определенности можно выделить четыре "элементарных" вида течения: внешнее обтекание, течение в следах, внутреннее течение и течение в струях. Течения в следах и струях, в общем, являются продолжением внешних и внутренних течений и, соответственно, формируются они из этих течений. Внешним считается течение вблизи тела, движущегося условно в бесконечном объеме (подводная лодка в океане, сверхзвуковой самолет в воздушном пространстве, метеорит, влетающий в атмосферу Земли). За собой движущееся тело оставляет шлейф, который называют либо "ближним", либо "дальним" следом, в зависимости от приближенности его к телу. Внутренними называются течения в соплах, каналах, резервуарах, ограниченных стенками. При этом вытекающие из этих аппаратов потоки называются струями.

Любое из этих видов течения является, как правило, турбулентным, так как содержит в качестве составляющих поступательное, вихревое и закрученное движения. Ламинарное, послойное течение является частным случаем турбулентного и в чистом виде встречается реже, как правило, в идеализированных, вялотекущих процессах, протекающих при низких скоростях (обтекание сферы, плоскости).

Разговор пойдет о внешнем обтекании различных тел, об обтекании тел условно простой и сложной формы, вообще о турбулентности сложных форм, поскольку даже обтекание тел простых форм приводит к сложным течениям.
Простыми считаются формы, обладающие максимальной симметрией. Самую большую степень симметрии имеет сфера - в этом случае говорят о сферической симметрии. Далее "в порядке убывания" можно вести речь об осевой симметрии (осесимметричное течение в сопле), плоской или зеркальной симметрии, циклической симметрии (лопатка и сектор в турбине), модульной симметрии (элемент теплового аккумулятора для солнечной энергодвигательной установки).

Не всегда рационально придавать аппаратам и движущимся объектам простую форму, чаще их стараются сделать максимально обтекаемыми, то есть обладающими наименьшим гидравлическим или аэродинамическим сопротивлением. При этом вопросы симметрии играют главенствующую роль. Вопросы обтекания правильнее всего начинать изучать на сфере, но возникающие при ее обтекании пространственные течения не всегда удается зафиксировать на фото- или видеопленку. Поэтому прибегают к исследованию обтекания цилиндра с осью, расположенной перпендикулярно направлению потока. Такое обтекание наиболее тщательно изучено и рассмотрено в литературе. Например, обтекание цилиндра дозвуковым потоком сжимаемой жидкости (газа), то есть потоком со скоростями, не превышающими скорость ударной волны давления или скорости распространения звука. Дозвуковое обтекание происходит при различных скоростях или, правильнее сказать, при различных режимах течения. При этом гидро- и газодинамика режима течения характеризуется специальным критерием Re, носящим имя знаменитого английского исследователя Осборна Рейнольдса. Этот критерий представляет собой отношение инерционных сил давления p = 0,5 u2 (здесь - плотность, u - скорость) к силам вязкого трения жидкости или газа вблизи обтекаемого тела: = u/d ( - вязкость, d - диаметр цилиндра). Превышение некоторого значения критерия Re сигнализирует о переходе к развитому турбулентному режиму течения. Начальная стадия - ламинарное течение. Это течение еще называют даламберовским. Великий математик и гидродинамик Даламбер, исследуя обтекание цилиндра, установил интереснейший факт (парадокс Даламбера): тело, двигаясь поступательно, прямолинейно и равномерно в жидкости, может не испытывать сопротивления с ее стороны! Реально это возможно только при весьма малых числах Рейнольдса. Уже при небольшом увеличении Re за цилиндром возникает донная область с разрежением. Линии тока в кормовой (донной) части начинают деформироваться, а разница давлений в носовой и кормовой частях увеличивается. Растет сопротивление потока. Далее с увеличением числа Рейнольдса за цилиндром начинают образовываться вихри, вращающиеся навстречу друг другу. С ростом Re их размеры и интенсивность вращения увеличиваются, а сопротивление потока растет. При достижении определенного режима течение в виде парных цилиндрических вихрей за обтекаемым цилиндром становится неустойчивым, и любая флуктуация приводит к появлению поперечное силы. В связи с этим вихри начинают "обходить" друг друга, располагаясь в шахматном порядке. Формируется новый устойчивый режим турбулентного течения, которое в литературе называется "дорожкой Кармана". Этот режим носит имя величайшего гидро- и газодинамика прошлого столетия Теодора Кармана.

Если дальше увеличивать число Рейнольдса (например, увеличивая скорость тела или потока), то за цилиндром можно получить развитую полномасштабную турбулентность, распространяющуюся в виде следа, сведения о тонкой структуре которого в литературе практически отсутствуют. В этой области возникают существенные пространственные течения. Выражаясь математическим языком - трехмерные течения, то есть зависящие от трех координат. И ситуация приходит к той, которая возникает при обтекании сферы. Может сложиться впечатление, что на этом все и закончено. Что нового качества, как скорость не увеличивай, мы не получим. На самом деле все происходит не так. С увеличением скорости обтекания, а значит с ростом числа Рейнольдса, мы все ближе подходим к скорости звука и, достигая ее, получаем предельное значения числа Рейнольдса для данного размера цилиндра. И тут возникает необходимость в новом критерии, определяющем режим течения. Этот критерий должен показывать во сколько раз упорядоченный поток, обтекающий цилиндр в определенном направлении, больше скорости распространения ударной волны в газообразной или жидкой среде.

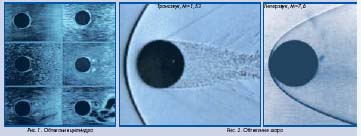
Из кинетической теории газов следует, что скорость распространения звука совпадает с тепловой скоростью движения молекул. Поэтому процесс распространения звуковой волны представляется как непосредственное передвижение молекул из области сгущения в область разрежения. Происходит обмен скоростями и "передача эстафеты" от одних молекул к другим. Другими словами, необходим критерий, определяющий степень отличия направленного потока газа от хаотического теплового движения молекул. Такой критерий в честь известного австрийского ученого назван числом Маха: М = u/a , где u - все та же скорость потока, а - скорость звука или приближенно скорость теплового движения. Понятно, что при достижении потоком скорости звука число Маха равно единице, а если оно больше единицы, то поток считается сверхзвуковым. Другой критерий, характеризующий сверхзвуковой поток, - это так называемый скоростной коэффициент = u/aкр. Здесь акр - это та же скорость звука в газе, но взятая при условии М = 1. Зачем потребовалось столько критериев - мы поймем дальше, а сейчас посмотрим, что происходит при обтекании того же самого цилиндра, но уже сверхзвуковым потоком. Цилиндр как бы "закрывается зонтиком от дождя". Появляется четкая тонкая граница, похожая на параболу, а сам цилиндр находится в фокусе этой параболы. Что же это за штучки такие? Откуда взялся "зонтик"? Все очень просто. Образовалась ударная волна. Она скачкообразно разделила поток на сверхзуковой и дозвуковой. Мы-то полагали, что цилиндр обтекается сверхзвуковым потоком, а он по-прежнему обтекается дозвуковым. И, более того, чем больше число Маха (а значит и ) сверхзвукового потока, тем меньше скорость (числа М и ) дозвукового потока: дозв = 1/ св.зв. Ближний след с увеличением числа Маха набегающего потока постепенно приближается к ламинарному.

Таким образом, самая "бурлящая" турбулентность сосредоточена в области чисел Маха, близких к единице и чисел Рейнольдса, максимальных для данного размера обтекаемого тела. Если число Рейнольдса отнести к его максимальному значению, то тогда и отношение Re/Reкр. также будет равно единице. Следует высказать одну очень важную мысль. Переход от сверхзвукового течения к дозвуковому может осуществляться только в случае "прямой" ударной волны, когда преграда расположена строго перпендикулярно по отношению к сверхзвуковому потоку. Если она расположена под углом, либо обтекается конус или хорошо обтекаемое тело, то образуется так называемый "косой скачок уплотнения". Проходя через него, поток остается сверхзвуковым, поэтому снижение скорости можно осуществлять постепенно, регулируя угол наклона. Вероятно, первая фотография, зафиксировавшая сверхзвуковой поток, была сделана самим Эрнестом Махом. Ему удалось запечатлеть полет бронзовой пули в воздушной среде. Пуля имела хорошо обтекаемую форму в носовой части и цилиндрическую по длине. Были зафиксированы коническая ударная волна и мелкомасштабная турбулентность в кормовой части. Аналогичная картина была получена позднее для течения вблизи ракеты. Коническая носовая часть, скругленная у вершины, цилиндрический корпус и оперение позволили продемонстрировать на модели сложную картину обтекания сверхзвуковым потоком и исследовать сопротивление.

Оптимизация сверхзвуковых форм показала, что наиболее выгодными являются заостренные тела, и в зависимости от скорости набегающего потока угол заострения может существенно изменить общее сопротивление движущегося в среде аппарата. При больших значениях чисел Маха течение называется гиперзвуковым. В теории такое течение рассматривается как некое предельное, стремящееся к течению с М . На самом деле его особенные свойства проявляются при сравнительно умеренных числах Маха. Так, например, при числах Маха больше пяти обтекание сферы и конуса имеет автомодельную зависимость коэффициента сопротивления сх от скорости набегающего потока.

При обтекании гиперзвуковым потоком различных осесимметричных тел угол наклона фронта скачка близок к углу отклонения потока в скачке, поэтому слой уплотненного газа, расположенный между фронтом скачка и поверхностью тела, оказывается очень тонким. При этом течение в следе за телом становится практически ламинарным.

Сверхзвуковое обтекание может существенно исказиться в случае, если тело находится не в условно бесконечном потоке, а в потоке, создаваемом сверхзвуковым соплом. Отраженные от стенок скачки уплотнения пересекаются с отраженными от тела ударными волнами. При определенных условиях такого обтекания возникает "висячая" (в потоке) ударная волна.

Приведенные картины сверх- и гиперзвукового обтекания тел показывают, что это течения весьма упорядоченные. Линии тока и линии скачков уплотнений либо прямые, либо имеют правильные очертания. В сверхзвуковом течении турбулентность отсутствует. Вихревые течения, кручение потока, а также любое пересечение линий тока неизбежно приводят к возникновению ударных волн и скачков уплотнения.

Рассмотренные выше случаи обтекания круглого цилиндра и случаи сверхзвукового течения являются наиболее простыми с точки зрения турбулентности. Более сложные случаи - это случай дозвукового обтекания несимметричных тел и несимметричного обтекания симметричных тел. Обтекание симметричного профиля крыла самолета, находящегося под некоторым углом к набегающему потоку (углом атаки) - типичный случай несимметричного обтекания. Течение ламинарное, поскольку отсутствуют пересекающиеся линии, области обратных токов и вращения. По сгущению линий тока можно судить об ускорении потока.

Трехмерное обтекание осесимметричного эллипсоида под углом атаки можно наблюдать при помощи разноцветных красок, подаваемых из специальных отверстий на поверхность тела. Ученым удалось зафиксировать уникальный момент обтекания тела со стороны кормовой части. Можно по-хорошему позавидовать везению экспериментаторов, нашедших еще одну устойчивую форму турбулентного течения и положивших ее в общую бесценную копилку знаний.

Еще большую сложность турбулентного течения демонстрирует картина обтекания вращающегося пропеллера. В ближнем следе зафиксирована циклическая картина на периферийной и внутренней частях винта самолета. Центральная донная часть заполнена течением с мелкомасштабной турбулентностью, а внутри кольцевой части между циклическими структурами расположена зона прямолинейного поступательного движения воздуха.

Внешне кажущееся хаотическим турбулентное течение является весьма упорядоченным периодическим течением, представляющим собой яркий пример волнового движения. Исследование турбулентности сложных форм необходимо как для общего понимания сложной структуры течения, так и для получения интегральных характеристик движения аппаратов в различных средах.