МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИНЦИПИАЛЬНО НОВЫХ ТИПОВ УСТРОЙСТВ

ФГУП "ЦИАМ им. П.И. Баранова": Владимир Скибин, генеральный директор, д.т.н.
Александр Крайко, начальник отдела, д.т.н.

 

C 1969 г. в ЦИАМ для решения нестационарных задач внутренней и внешней аэродинамики широко и успешно применяются монотонные разностные схемы "распадного" типа. В 1972 г. в ЦИАМ предложена подобная схема "маршевого" счета двух- и трехмерных сверхзвуковых стационарных течений, не имевшая конкурентов по эффективности и работоспособности. Расчеты, выполненные в нашем институте с применением "распадных" схем, легли в основу вышедшей в 1976 г. монографии: Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. "Численное решение многомерных задач газовой динамики". Став настольной книгой отечественных аэрогазодинамиков, эта монография обеспечила заметный прогресс вычислительной газовой динамики. На Западе схемы такого типа получили широкое распространение примерно с десятилетней задержкой. Тем временем в ЦИАМ численные методы совершенствовались и развивались. В настоящее время на основе "распадных" схем созданы эффективные методы интегрирования уравнений Эйлера, Навье-Стокса и Рейнольдса.

Вычислительная газовая динамика и математическое моделирование особенно ценны при исследовании устройств, призванных обеспечить реализацию новых принципов и конструктивных схем. Подобное положение обусловлено рядом причин, прежде всего - отсутствием соответствующего опыта конструирования и эксплуатации. Для экспериментальных исследований моделей таких объектов нужны принципиально новые, дорогостоящие стенды. Нередко модельные эксперименты не обеспечивают необходимых условий подобия. В подобных случаях вычислительная газовая динамика и математическое моделирование дают основную, а подчас и единственную, причем чрезвычайно ценную информацию об ожидаемых локальных и интегральных характеристиках предлагаемых устройств, областях их применения, целесообразности создания и направлениях дальнейшего развития.

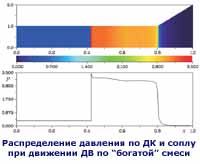
В ЦИАМ предложена оригинальная схема сверхзвукового пульсирующего детонационного прямоточного двигателя (СПДПД). Его главные отличия: по всему тракту двигателя движется сверхзвуковой поток воздуха и горючей смеси; детонационная волна (ДВ) распространяется навстречу сменяющим друг друга сверхзвуковым потокам "богатых" горючих смесей с изменением типа смеси регулированием подачи топлива; пульсирующий процесс обеспечивается движением ДВ в богатой смеси по детонационной камере (ДК) к воздухозаборнику и последующим ее сносом сверхзвуковым потоком бедной смеси к соплу; непрерывность детонации исключает необходимость во внешнем источнике ее инициирования на каждом цикле (такой источник нужен только при запуске).

Эти свойства определяют сверхзвуковой диапазон чисел Маха полета М0, в котором применим СПДПД: для водородо-воздушного варианта это 4,5 < М0 < 7. Иначе говоря, СПДПД предназначен для работы в следующем диапазоне М0 (после диапазона, характерного для ПВРД), который предстоит освоить воздушно-реактивным двигателям. В отличие от СПДПД пульсирующие прямоточные ВРД других схем, в которых осуществляется торможение воздуха до дозвуковой скорости, могут применяться от взлета до умеренных сверхзвуковых скоростей.

В ЦИАМ созданы эквивалентные по основным допущениям математические модели СПДПД, ПВРД и СПВРД. Сопоставляя результаты моделирования, можно сделать вывод о некотором преимуществе СПДПД над ПВРД и СПВРД по удельному импульсу при меньшем торможении сверхзвукового потока и, как следствие, о существенно меньших плотности тока и теплонапряженности тракта двигателя (в разы по сравнению с СПВРД и почти на порядок - с ПВРД).

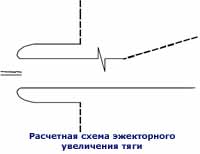
Пульсирующий эжекторный увеличитель тяги. Интерес к пульсирующему эжекторному увеличителю тяги восходит к середине ХХ века. В свете последних разработок одно из возможных его применений - разгон летательного аппарата до чисел Маха М0 рабочего диапазона СПДПД с использованием топливных пилонов СПДПД в качестве пульсирующих ракетных двигателей, а тракта СПДПД - как эжекторного увеличителя.

Условия, определяющие режим истечения активного газа в эжекторном увеличителе тяги, сводились к заданию его полной температуры и расхода ступенчатой периодической функцией.

Рассмотрим эжекторы с сужающимся соплом и с соплами Лаваля (М = Мрi = 1,5 и 2,5). Все сопла имеют одинаковую площадь. У стационарного увеличителя максимальный прирост удельного импульса достигает 20…60 %, снижаясь при больших расходах до 5%. Таким образом стационарный увеличитель эффективен тогда, когда удельный импульс сопла без эжектора составляет 10…20 % его максимальной величины.

Все режимы, определяемые средним расходом, можно разбить на три участка. Первый участок соответствует значениям среднего расхода, при которых в стационарном сопле реализуется существенно сверхкритический перепад. Здесь прирост удельного импульса от применения пульсирующего увеличителя составляет не более 10…20%. Второму участку соответствует область околокритических перепадов стационарного сопла. Здесь преимущество пульсирующего увеличителя может достигать величин порядка 100 %. Если, однако, допустить возможность работы стационарного сопла при параметрах, близких к пиковым пульсирующего эжектора, то оно даже без эжектора будет иметь удельный импульс, близкий к импульсу пульсирующего увеличителя. К тому же его размер при одинаковой полной тяге будет в разы меньше, чем размер сопла пульсирующего увеличителя. Сказанное, тем не менее, не означает, что при средних расходах, отвечающих сверхкритическим и околокритическим стационарным перепадам, пульсирующий увеличитель не может найти применения. Как отмечалось выше, он может оказаться востребованным при старте и разгоне СПДПД, предназначенного для работы при сравнительно больших числах Маха. На третьем участке с докритическими средними давлениями пульсирующий эжектор обеспечивает значительные приросты удельного импульса, которые нельзя существенно уменьшить умеренным варьированием рабочих параметров стационарных аналогов. Здесь пульсирующие увеличители даже при пиковых расходах, как правило, работают на докритических перепадах, а отвечающие тем же расходам сужающиеся стационарные сопла являются расчетными и как изолированные стационарные практически не улучшаемыми.

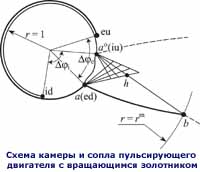
Пульсирующий двигатель с вращающимся золотником. Камера сгорания такого двигателя, образованна двумя соосными не полностью замкнутыми круговыми цилиндрами. Сопло несимметричного типа. Внешний цилиндр (корпус) неподвижен. Внутренний (золотник) вращается против часовой стрелки. До момента времени открытия "минимального сечения" - т.е. совпадения передней ("верхней") по вращению границы разреза золотника с задней ("нижней") границей разреза корпуса параметры газа ("продуктов сгорания") в закрытой камере однородны, скорость равна нулю, а перепад давления сверхкритический. После открытия щели через нее начинается истечение газа с разгоном до сверхзвуковой скорости. Контур сопла нужно выбрать таким, чтобы при заданных габаритах величина импульса тяги сопла была максимальна.

Параметры в камере по мере истечения газа изменяются, и перед ее закрытием из-за малости перепада давления скорость истечения может стать сравнительно малой. Данное обстоятельство и опыт профилирования сопел делает почти очевидным выбор в пользу несимметричного сопла. В рамках развитых в ЦИАМ подходов контуры несимметричных сопел, которые реализуют максимум тяги, осредненной по нескольким частям периода раскрытия щели, строятся по результатам расчетов методом характеристик как "средневзвешенные по тяге" для разных моментов времени. Окончательно процесс истечения из камеры и силы, действующие на все устройство, рассчитываются интегрированием двумерных нестационарных уравнений Эйлера. Изменение параметров торможения газа описывается "элементарной теорией". В ее основе лежат предположения о квазистационарности, изоэнтропичности и изоэнергетичности истечения через зависящее от времени минимальное сечение (щель).

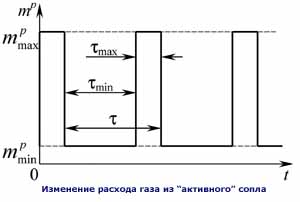В отличие от процесса истечения из щели течение вокруг всего устройства нестационарное - периодическое с периодом, который определяется вращением золотника. Нестационарные добавки, связанные с интегральным воздействием (за период по внешним обтекаемым поверхностям) нестационарных колебаний давления, сильно сказываются на потерях импульса.

Пульсирующий лазерный движитель. В лазерном движителе параболическое зеркало фокусирует луч находящегося вне летательного аппарата (ЛА) лазера в "центр" расширяющегося канала (сопла), а пульсирующий режим работы лазера позволяет в качестве рабочего тела использовать среду, окружающую ЛА. Среди проблем, связанных с таким движителем, - определение оптимальной частоты ("скважности") и интенсивности лазерного импульса, а также выбор оптимальных длины, степени расширения и формы сопла. Близкая к оптимальной форма сопла была построена "прямым" методом с помощью так называемого "генетического алгоритма".

"Волновой ротор" ("wave rotor"). Волновой ротор (ВР) - устройство, предназначенное для повышения максимальной температуры цикла (и термодинамического к.п.д.) энергетических и силовых установок при сохранении неизменной температуры газа перед турбиной - самым теплонапряженным элементом.

Сложность математического описания ВР, не имеющая аналогов в приложениях к другим элементам энергоустановок (соплам, диффузорам, венцам турбин и компрессоров, камерам сгорания), обусловлена тем, что течение в нем одновременно нестационарное и высокоскоростное. По этой причине для ВР нет теории, элементарной и достаточно точной в той же степени, как элементарная теория сопел и диффузоров, модель радиально уравновешенного течения в лопаточных венцах или термодинамическая теория тепловых машин.

Существенно упрощает моделирование рабочих режимов ВР то, что при нестационарном течении в каждом канале ВР все они имеют идентичную историю. Следствием такой идентичности является квазистационарность течения в ВР в целом, включая порты. При моделировании рабочих режимов ВР отмеченное обстоятельство позволяет ограничиться расчетом нестационарного течения в одном канале ВР, совершающем периодическое движение мимо портов и закрытых участков кожуха. Без учета эффектов неодномерности и неидеальности течения отличие расчетных и экспериментальных характеристик ВР получается недопустимо большим. Важнейшие из них - обусловленное вращением ВР изменение параметров при течении газа из канала ВР в порты и в противоположном направлении, немгновенное раскрытие и закрытие окон, трение о стенки канала и перетекание газа из канала во внутренний объем колеса ВР через зазор между его открытыми концами и стенками кожуха (и наоборот).

Расчетные характеристики ВР нуждаются в подтверждении экспериментальными данными. Главная проблема при этом состоит в неполноте содержащихся в доступных публикациях сведений о геометрических и режимных параметрах, соответствующих приводимым экспериментальным и расчетным характеристикам. Относительно полный набор таких данных есть для трехпортовых ВР, экспериментально исследованных в NASA и в Power Jets Corporation. Сравнения с этими данными результатов, полученных с использованием математических моделей ЦИАМ и Центра им. Льюиса, показали, что первая модель не уступает, а чаще описывает эксперимент лучше, чем вторая.

"Инерционный термояд". Один из ключевых моментов при реализации инерционного управляемого термоядерного синтеза является обеспечение сверхвысокого сжатия "мишени" - шарика из термоядерного материала лазерным или иным излучением с минимальными энергетическими затратами. Обычно оценки ожидаемых затрат опираются на автомодельное решение о сжатии идеального (невязкого и нетеплопроводного) газа сферическим или цилиндрическим поршнем. В указанном решении работа сжатия идет на увеличение и внутренней, и кинетической энергии сжимаемого материала, причем для любой конечной степени сжатия распределение параметров внутри сжатого объема сильно неравномерно. Поэтому энергозатраты, получающиеся при использовании такого решения, далеки от оптимальных.

В задаче нестационарного сжатия покоящегося однородного идеального газа по энергетическим соображениям наилучшим представляется сжатие за заданное время tf до заданной средней плотности f = c 0, где 0 - начальная плотность, а степень сжатия c >1, с минимальной работой поршня. В 1993 г. А.Н. Крайко решил задачу безударного сжатия газа плоским, цилиндрическим или сферическим поршнем в точной постановке для произвольного времени tf. Наиболее интересный результат построенного решения - обнаружение возможности изоэнтропического сжатия из покоя в покой. Для его реализации время сжатия tf должно быть не меньше некоторой величины, по порядку величины близкой к времени пробега звуковой волны от поршня до центра начального объема.

На первый взгляд, возможность построения реализующей сжатие из покоя в покой (СПП) траектории представляется проблематичной. Данная проблема, однако, имеет весьма простое решение - следствие инвариантности уравнений и условий, которые описывают безударные одномерные течения идеального газа относительно произвольного сдвига начала отсчета времени и одновременного изменения знаков времени и r -компоненты скорости. После соответствующего сдвига и указанного изменения знаков задача сжатия становится задачей расширения. Решение этой задачи сводится к последовательному решению двух стандартных задач метода характеристик.

Для реализации управляемого термоядерного синтеза плотность термоядерной мишени нужно увеличить в тысячи раз, а температуру поднять до (3…10)·107 K. Таким образом при степени изоэнтропического сжатия порядка 104 относительное увеличение температуры составляет около 102. В противоположность этому при сжатии сильной ударной волной (УВ), идущей к центру (оси) симметрии и отражающейся от него, можно достичь любого повышения температуры при ограниченном сжатии. В общем случае с уменьшением радиуса УВ процесс сжатия описывается автомодельным решением К. Гудерлея. Для обеспечения требуемых параметров нужно к С--характеристике, приходящей в центр сжимаемого объема одновременно с идущей туда же УВ, пристроить центрированную волну сжатия, т.е. найти реализующую их траекторию границы сжимаемого объема (сферического или цилиндрического поршня). Недавно одному из авторов данной статьи удалось построить решение этой далеко не простой задачи.

Авторы признательны В.Г. Александрову, Д.Н. Малову, К.С. Пьянкову, Н.И. Тилляевой и М.Н. Топоркову, результаты исследований которых составили основные иллюстрации данной статьи.