ТУРБУЛЕНТНОСТЬ В СЭДУ

Юрий Михайлович Кочетков, д.т.н.

 

Наиболее критичным элементом в солнечной энергодвигательной установке является тепловой аккумулятор, выполненный в виде коаксиальных графитовых модулей с щелевыми каналами. Турбулентность в этих каналах определяется особенностями течения рабочего тела (водорода) при теплоотдаче со стороны нагретых стенок и процессом гетерогенного разрушения стенок модуля теплового аккумулятора. В процессе расчётных исследований обнаружено локализованное решение, идентифицированное как тепловой солитон и конкретизирована переходная область между областями, характеризующими кинетический и диффузионный режимы гетерогенного окисления - область динамического режима.

Одним из наиболее энергетически эффективных и экономически выгодных способов выведения космических аппаратов (КА) на геостационарную орбиту (ГСО), является солнечная энергодвигательная установка (СЭДУ). Принцип действия такой установки основан на предварительном нагреве рабочего тела (водорода) до температуры 1500 К и последующей подаче его в малогабаритный ЖРД в качестве компонента. Такой нагрев повышает величину удельного импульса тяги практически в 2 раза. Нагрев осуществляется с помощью омического разогрева теплового аккумулятора энергией, полученной от Солнца при помощи солнечных батарей и преобразованной в электрическую энергию постоянного тока. В отличие от ЭРД, которые непрерывно питаются солнечной энергией в процессе всего времени полёта, а аппараты на их основе движутся по спирали в сторону ГСО, в СЭДУ эта энергия накапливается и превращается в импульс тяги дискретно в момент прохождения КА точки перигея. Космический аппарат после каждого импульса переходит на более вытянутую эллиптическую орбиту с фокусом в центре Земли, и после определенного набора циклов касается ГСО апогейной частью эллипса. В этот момент дается последний импульс, орбита становится круговой и работа ЖРД прекращается. Накопление тепловой энергии в аккумуляторе (режим "заряд") происходит непрерывно от момента реализации одного импульса до другого. В процессе импульсов холодный водород из баков поступает в каналы теплового аккумулятора, забирает от него тепло, нагревается и поступает через форсуночную головку в камеру сгорания. Тепловой аккумулятор при этом работает в режиме "разряд" [1]. Такая многоимпульсная схема выведения предполагает надежную работу всех элементов и узлов двигательного контура СЭДУ. Принципиальным элементом этого контура, определяющим эффективность всей двигательной установки, является тепловой аккумулятор, который испытывает за время работы на орбите длительные (до 600 с) многоцикловые (до 300 циклов) тепловые нагружения и химическое воздействие на аккумулирующие блоки.

Тепловой аккумулятор [2] представляет собой модульную конструкцию, состоящую из нескольких десятков углеграфитовых модулей с щелевыми каналами для протока водорода, объединенных сложным коллектором (рис. 1), который обеспечивает равномерную подачу расхода водорода в каждый канал. Коллектор представляет собой металлическую конструкцию, соединенную герметично с графитовыми блоками. В процессе работы герметичность соединения не нарушается благодаря подвижности сильфонов, компенсирующих перемещение при температурных расширениях металлических деталей коллектора (лантанированный молибден) и графитовых модулей (силицированный графит ПРОГ-2400). Щелевая конструкция графитового модуля выполнена таким образом, что тепловой поток с внешней и внутренней стороны канала всегда остается одинаковым благодаря равенству масс внешней и внутренней стенок. Одним из достижений в области технологий явилось изготовление в печах графитовых модулей большой длины (до 1 м) (рис. 2). Нагрев модулей аккумулятора осуществляется графитовым электрическим нагревателем, расположенным в центре аккумулятора. Аккумулятор теплоизолирован от внешней среды экранно-вакуумной тепловой изоляцией (ЭВТИ) на основе углеродной ткани и муллитовой ваты. Аккумулятор для СЭДУ был разработан и доведён до экспериментального образца натурного изделия. Были проведены все необходимые испытания в подтверждение надежности его работы. Анализ испытаний показал, что в процессе работы модулей теплового аккумулятора происходит разрушение и унос графитовых стенок под воздействием водорода. Поэтому возникла необходимость количественных оценок величин уносов, которые влияют на режим течения рабочего тела. Поток в каналах мог становиться турбулентным и увеличивать гидродинамическое сопротивление. В связи с этим анализ турбулентных течений оказалось целесообразным проводить с учётом теплоподвода со стороны нагретой стенки модуля и уносов углерода при взаимодействии с активным водородом.

Турбулентность в длинных каналах с теплоподводом

Задача исследования турбулентных течений в длинных щелевых каналах между коаксиальными цилиндрами и с теплоподводом может быть решена после нахождения чисел Рейнольдса вдоль канала в течение всего времени разряда теплового аккумулятора. Принципиальным является то, что подвод тепла со стороны стенки к потоку приводит к увеличению числа Рейнольдса и интенсифицирует турбулентность:

dRe/Re =(1-M²)^-1a^-2(k-1) Q_max dq*,

где q* - относительный тепловой поток; Q_max - тепло, подведенное к входной части модуля теплового аккумулятора; М и а - число Маха и местная скорость звука.

Для описания процесса теплопереноса решается нестационарное уравнение теплопроводности для цилиндрической расчётной области. Оно является нелинейным. Общая система, описывающая задачу совместного охлаждения вкладыша и нагрева рабочего тела может быть записана в безразмерном виде, совместно с граничными условиями третьего рода. Решение такой нелинейной системы уравнений возможно с использованием расчётных программ. Присутствие нелинейного члена в уравнении теплопроводности второго порядка означает, что среди прочих стандартных решений имеются локализованные решения в виде солитонов, то есть такие устойчивые решения, когда дисперсия искомого параметра конкурирует с его нелинейностью. При этом нелинейность приобретает физический смысл, обратный по значению дисперсии. Другими словами дисперсия размывает искомый параметр, а нелинейность его локализует.

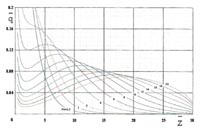В данной задаче искомым параметром является относительная величина теплового потока от стенки к рабочему телу q*. Численное решение записанной системы уравнений позволило проанализировать поведение этого параметра в зависимости от осевой координаты аккумулирующего модуля и времени его разряда. Решение представлено на рис. 3. Все параметры для общности приведены в безразмерном виде, причем безразмерное время, число Фурье, построено по наружному радиусу щелевого канала. Из рис. 3 видно, что семейство расчётных линий представляет собой набор немонотонных кривых с максимумом, продвигающимся в направлении к срезу сопла с увеличением времени разряда. Очевидно, что такой эффект может возникать при достаточно длинных каналах. Если каналы короткие, то кривая - монотонно падающая.

Полученное решение в виде такой устойчивой тепловой волны является упомянутым ранее локализованным решением - тепловым солитоном. Наличие теплового солитона неизбежно вносит свои особенности в турбулентное движение потока водорода по каналу модуля теплового аккумулятора. При этом возможно возникновение локальных зон турбулентности в определенных местах канала. Эти зоны могут передвигаться к срезу канала, отслеживая движение теплового солитона.

Турбулентность при гетерогенном разрушении обтекаемой поверхности

Разрушение углеродных стенок модулей теплового аккумулятора под воздействием агрессивных потоков водорода происходит в гетерогенном режиме. Вблизи поверхности стенки канала реакция водорода с углеродом происходит в пять стадий: 1 - диффузионный перенос водорода к поверхности из углерода; 2 - адсорбция водорода на углеродной поверхности; 3 - хемосорбция и образование активированных комплексов; 4 - десорбция метана с поверхности; 5 - транспортировка метана в поток водорода. Разложение реакции на элементарные стадии позволяет записать достаточно простую систему уравнений химических реакций и теоретически рассчитать их скорость. Для этого необходимо помимо уравнений сохранения определить константы скоростей соответствующих реакций к(T). Оценка констант скоростей реакций может быть выполнена методами статистической термодинамики [3] в зависимости от температуры и других параметров реактантов. Обычно структура констант равновесия содержит экспоненциальный член с аргументом в виде комплекса, представляющего собой отношение энергии активации к произведению универсальной газовой постоянной и температуры. Суммарная скорость гетерогенной реакции определяется скоростью её самой медленной стадии. Если наиболее медленными оказываются стадии 1 и 5, то процесс взаимодействия протекает в диффузионной области. В этом случае можно считать, что химические реакции протекают со скоростью диффузии и влияние кинетики этих реакций можно не учитывать. В диффузионной области зависимость от температуры отсутствует. Если наиболее медленными оказываются стадии 2, 3 или 4, то процесс происходит в кинетической области. Балансовые уравнения и кинетические соотношения были систематизированы и представлены А.В. Каревским в его кандидатской диссертации в виде методики расчёта. 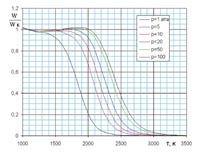Систематические расчёты, проведенные им с использованием этой методики, показали существенную зависимость скорости гетерогенной реакции от температуры и давления рабочего тела вблизи обтекаемой поверхности аккумулирующего модуля. Расчётные результаты удалось компактно уложить в семейство расслаивающихся кривых после нормирования значения скорости гетерогенной реакции относительно аналогичной скорости реакции в кинетическом режиме (рис. 4). В этом случае зависимость относительной скорости гетерогенной реакции оказалась разбитой на три области, соответствующие трём режимам: кинетическому (W/Wк = 1), диффузионному (W/Wк = 0) и переходному. Последний режим логично назвать динамическим, так как в этой области существенно проявляется зависимость от давления. Появилась возможность конкретизировать диапазоны температур, в которых реализуется этот режим.

Традиционно наступление кинетического и диффузионного режима связывают с критерием знаменитого немецкого химика Герхарда Дамкёлера (1908-1944 гг.), который определяется отношением скорости химической реакции к скорости диффузии компонентов в зону реакции:

Da=к(T)c^n-1L²D^-1,

где c и n - концентрация компонентов у поверхности и порядок реакции; L - характерный линейный размер процесса; D - коэффициент диффузии. С учетом особенностей конструкции теплового аккумулятора и рабочего тела получим зависимость критерия Дамкёлера от давления и температуры:

lnDa=26,6 + lnP - 0,5lnT - 50400T^-1.

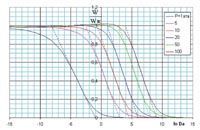Основываясь на предыдущих расчётах, воспроизведём зависимость относительной скорости гетерогенной реакции от критерия Дамкёлера (рис. 5). Из рисунка видно, что эта зависимость практически линейная за исключением областей сопряжения вблизи единицы и нуля по ординате. Из этой зависимости легко определяются аппроксимационные соотношения для области динамического режима:

W/Wк=0,4lnP/P₀ - 0,2lnDa.

Здесь P₀ - давление внешней среды. В силу того, что наклон динамических кривых к оси практически для большинства случаев одинаковый, возможно определить диапазоны, в которых реализуется динамический режим. Правая граница, соответствующая началу диффузионного режима, определится как

Da_пр =P²/P²₀ ,

а левая - концу кинетического:

lnDa_л=2lnP/P₀ - 5.

Так, например, для давления P = 5 ата динамический режим гетерогенной реакции водорода с твёрдой поверхностью углерода находится в диапазоне: 0,17 <= Da <= 25. В результате проведенных исследований появилась возможность достаточно корректного определения скоростей гетерогенных реакций водорода с графитом, а значит величин массовых скоростей уносов материалов конструкции теплового аккумулятора. В предыдущей статье [4] было показано, что величина массовой скорости уноса является функцией от окислительного потенциала, давления и температуры. Именно эти параметры определяют интенсификацию турбулентности в тепловом аккумуляторе при гетерогенном разрушении его стенок.

Литература

1. В.Н. Акимов, Н.И. Архангельский, А.С. Коротеев и Е.П. Кузьмин. Солнечная энергодвигательная установка с электронагревным тепловым аккумулятором и дожиганием рабочего тела // Полёт, № 2, 1998.
2. Ю.М. Кочетков, А.В. Каревский, А.К. Соловьёв, Ю.А. Ошев и др. Тепловой аккумулятор для нагрева рабочего тела. Патент РФ № 2224187, 2004.
3. Н.Н. Семёнов. О некоторых проблемах химической кинетики и реакционной способности. М.: Государственное издательство физико-математической литературы, 1962.
4. Ю.М. Кочетков. Турбулентность в ГРД и ГРРД // Двигатель, № 1, 2011.