СРЫВНЫЕ ТЕЧЕНИЯ ЖИДКОСТНОЙ И ГАЗОВОЙ ФАЗ

Евгений Николаевич Беляев,  к.т.н., МАИ

Валерий Васильевич Черваков,  д.т.н., МАИ

 

 

Создание новой ракетно-космической техники всегда сопряжено с риском принятия неверных решений, приводящих к тяжелым аварийным ситуациям. Без этого не обходится ни одна из отраслей промышленности, будь то авиационная, атомная или судостроительная промышленность. Путь в космическое пространство вымощен обломками ракетно-космической техники, разрушением испытательных стендов и стартовых комплексов, омрачен гибелью отважных космонавтов и астронавтов. Одной из причин тяжелых аварийных ситуаций, совершенно непредсказуемых, являлось возникновение колебаний элементов конструкции или давлений компонентов топлива в жидкостном ракетном двигателе (ЖРД) приводившие к его разрушению. Причиной возникновения таких колебаний были разные, в их числе, срывы вихрей при течении жидкостной или газовой фаз. В технике, и в первую очередь, в авиационной, с этой проблемой столкнулись 1930-х гг., когда по миру прокатилась волна странных аварий при испытаниях скоростных самолетов. Летчики испытатели, которым посчастливилось остаться в живых, и очевидцы наблюдали почти одну и ту же картину: самолет летел нормально, как вдруг какая-то неведомая сила, будто взрывом, разрушала машину. Этому всегда предшествовало интенсивное увеличение вибраций самолета с нарастающей амплитудой. Это таинственное и грозное явление назвали "флаттер" (от английского flutter - дрожание). Ученые, и в частности М.В. Келдыш, довольно быстро разобрались, что флаттер порождается взаимодействием в конструкции упругих, инерционных и аэродинамических сил.

Плохое обтекание крыла самолета может привести к неустойчивости - срывному флаттеру. На современных самолётах он может произойти в условиях обледенения, когда поверхность крыла, в частности его передняя кромка, покрывается ледяной коркой произвольной формы. Характер обтекания резко ухудшается, и за крылом может формироваться периодическая система вихрей - “дорожка Кармана”, которая вызывает колебания крыла. Фон Карманом экспериментально установлено [1], что при обтекании цилиндрических тел, или плоских пластин, установленных под некоторым углом к набегающему потоку, происходят поперечные колебания зоны отрыва течения (срыв вихрей). При этом зона пониженного давления оказывается то с одной, то с другой стороны от направления движения, в результате на тело действует не только продольная сила лобового сопротивления, но и переменная поперечная сила.

Явление отрыва связано с большими градиентами давления и скорости течения в пограничном слое. Отрыв потока обычно возникает в точках максимальной скорости и, следовательно, минимального давления, после чего это низкое давление доминирует во всей зоне отрыва ниже по течению [2].

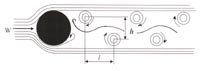Карман теоретически показал, что картина расположения вихрей (вихревых следов) стабильна, если отношение поперечного расстояния между ними h к продольному расстоянию l (рис. 1) составляет h/l = 0,28.

Вихревые следы встречаются повсеместно. Их можно создать в лабораторных условиях, можно наблюдать в природе.

Говоря о срывном флаттере, следует отметить, что чаще всего он возникает тогда, когда частота схода вихрей приближается к одной из собственных частот конструкции. В этом случае возникают резонансные колебания, которые могут приводить к разрушению конструкции.

Срывной флаттер наблюдался неоднократно у целого ряда технических сооружений: многих подвесных мостов, заводских труб, винтов вертолетов, перископов подводных лодок, лопаток компрессоров, турбин в турбореактивных двигателях, на днищах ракет, проводах высоковольтных линий и т.п. Он приводил к различным катастрофам, среди наиболее известных, это разрушение Такомского моста [3]. Случилось это в ноябре 1940 года в США. Такомский мост простоял всего несколько месяцев и был полностью разрушен 7 ноября (рис. 2). Причиной разрушения стали многочисленные дорожки Кармана, которые отрывались от силовых тросов, напоминающих огромные вертикальные струны. При скорости ветра 19 м/с, установились одноузловые изгибно-крутильные колебания полотна моста с такой амплитудой, что угол наклона проезжей части к горизонту достигал 45°. После часа таких колебаний часть проезжего полотна отломилась и рухнула в воду.

Частота срыва вихрей определяется числом Струхаля

Sh=f×l/W  ,

где  W - скорость набегающего потока,
f - частота вихреобразования,
l  - характерный размер (например, диаметр цилиндра или ширина пластины) [1].

Число Струхаля - безразмерная величина, один из критериев подобия нестационарных течений жидкостей и газов, характеризующий постоянство протекания процессов во времени.

Экспериментально установлено, что число Струхаля является безразмерной частотой генерации вихрей и связано с числом Рейнольдса для потока, порождающего след. Для ламинарного режима (режим I), переходного режима (режим II) и третьего режима (режим III), в котором поток не реагирует с одной единственной частотой, но число Струхаля соответствует частоте с максимальной энергией соотношением Sh = 0,2175 - 5,1064/Re для ламинарного режима течения (до Re = 200) и  Sh = 0,212 - 2,7/Re  для больших значений Re равных 400 и выше. Последняя аппроксимация содержит предельное (0,212) число Струхаля при больших значения числа Re [4].

В работе [4] приведены экспериментальные данные (рис. 3), по которым получены выше приведенные соотношения между числами Струхаля и Рейнольдса.

Проблеме срыва вихрей и генерации звука посвящено очень большое количество работ начиная с конца ХIX века по сегодняшний день. На рис. 4 приведены экспериментальные данные, полученные разными авторами и в разное время [5], зависимости числа Струхаля от числа Рейнольдса.

На графике хорошо видно, что в диапазоне 4·102 < Re < 4·105, число Струхаля лежит в интервале от 0,18 до 0,22. Это однозначно указывает на то, что в рассматриваемом диапазоне чисел Рейнольдса частота эоловых тонов [6] прямо пропорциональна скорости потока среды.

И только при очень малых или очень больших числах Рейнольдса число Струхаля уменьшается или, соответственно, увеличивается.

Как ранее было отмечено, на режиме III (рис. 3) поток реагирует не одной единственной частотой, а целым спектром обертонов. Это хорошо было показано W. Holle [5]. Им были исследованы и экспериментально получены спектры звуков, возникающих при размещении длинного тонкого стержня в воздушном потоке. На рис. 5 приведен спектр звука [5], генерируемого потоком при обтекании со скоростью 33 м/с стержня диаметром 5 мм. Эта скорость потока соответствует числу Рейнольдса, равному 1,08·104. Частота f основного тона составила 1330 Гц, что соответствует числу Струхаля, равному 0,2.
Кроме основного тона в спектре присутствовали две высшие гармоники. Первая из них имела частоту f = 2660 Гц, а вторая f = 3990 Гц, но существенно более низкого энергетического уровня  (на L = 20 и 15 дБ соответственно). Это дало основание для вывода о том, что формулу Струхаля следует обобщить, чтобы учесть гармоники основных частот:

f_n=Sh·W·n/l,
где n =1, 2, 3...

Со срывными явлениями связаны некоторые гипотезы, в частности появление кораблей с мертвым или полностью отсутствующим экипажем. Полагается, что в случае шторма на море, если морские волны рассматривать в первом приближении бесконечными цилиндрами, то можно прийти к выводу, что в этом случае над морем (а также в воде) будут возникать колебания с частотой 6...13 Гц. Эти звуки, которые, слабо поглощаясь, распространяются в море и над ним на огромные расстояния, могут быть прогностическим фактором. Их появление является сигналом для морских и наземных животных и птиц. Многие ракообразные, медузы, воспринимают эти колебания и спешат укрыться или удалиться от берега, где волны штормового прибоя могут разбить их о скалы.

Небезразличен к этим колебаниям и человек. Этот диапазон частот совпадает с ритмами головного мозга, основных физиологических процессов. Французский ученый Гавро показал, что для человека они могут быть смертельными или вызвать серьезные нервно-психические и соматические расстройства, вплоть до паралича сердечной мышцы. Хотя до сей поры пока так и неясно, каким же образом человек воспринимает эти колебания - ведь ухо человека ощутить их неспособно.

Срывные явления нашли применение в технике, в частности это явление используется в вихревых расходомерах [7]. Поскольку в определенном диапазоне чисел Рейнольдса число Струхаля практически равно константе, благодаря чему получается, что коэффициент преобразования скорости потока в частоту вихрей становится не зависящим ни от плотности, ни от вязкости измеряемой среды и одинаков для всех типов сред.

На ветровой резонанс рассчитываются мосты, высотные здания и сооружения, дымовые трубы и т.п.

При экспериментальной отработке ЖРД бывали случаи аварийного останова двигателей на огневых стендах связанные именно со срывными явлениями в гидравлических и газовых магистралях. Они происходили из-за разрушения: редукторов, дроссельных заслонок, стопорных "лепестков" прокладок, термопар и прочих элементов. Попадание частиц (частей) разрушенных элементов в турбину, как правило, приводило к ее возгоранию.

Современное состояние теоретических и экспериментальных исследований в области срывных течений и механических колебаний позволяют заранее проанализировать их возможные взаимосвязи в разрабатываемой конструкции [9]. Учитывая, что при отработке новых ЖРД, их количество, используемое при доводочных испытаниях, исчисляется единицами вопросам вихреобразования необходимо уделять самое пристальное внимание.

ЭОЛОВЫЕ ТОНА - звуки ЭОЛОВОЙ АРФЫ  - (по имени древнегреческого бога ветров Эола). Струны, настроенные в унисон и колеблемые движением воздуха, издают обертоны одного общего тона; громкость звука зависит от силы ветра [8].

Человеческое ухо способно уловить звуки далеко не всех частот. Считается, что звуки частотой ниже 20 Гц и выше 20 кГц мы не слышим. Реально диапазон нашего звукового восприятия даже более узкий, так как с возрастом человек начинает хуже слышать высокие частоты [8].

Келдыш, Мстислав Всеволодович (10.02.1911 - 24.06.1978) - выдающийся советский ученый в области математики и механики. После окончания в 1931 г. Московского университета работал в ЦАГИ. Внес решающий вклад в решение проблем флаттера. Основные труды в области математики, механики и аэрогазодинамики летательных аппаратов. Келдыш внес выдающийся вклад в развитие вычислительной и машинной математики в СССР, в создание эффективных методов расчета задач атомной и космической техники. В Московском государственном университете учреждена стипендия имени М.В. Келдыша. Его имя носит Институт прикладной математики. В его честь назван один из кратеров на Луне [8].

КАРМАН, ТЕОДОР фон (Kаrmаn, Theodore von) (11.05.1881-05.05.1963) - американский инженер. Среди наиболее известных работ Кармана - теоретические и экспериментальные исследования в области аэро-, гидро- и термодинамики, прочности авиационных конструкций и материалов, теории пластичности и упругости, сопротивления материалов. Разработал ряд математических методов прочностных расчетов, решение даже чисто академических задач всегда сопровождал выводами и результатами, которые имели значение для инженерной практики. Карман был одним из основателей и первым президентом (1960-1961) Международной академии астронавтики, консультантом ряда крупных аэрокосмических фирм, членом многих иностранных академий и научных обществ. В 1948 была учреждена международная премия его имени, в его честь назван один из кратеров на Луне [8].

СТРУХАЛЬ, ВИНСЕНС (Strouhal, Vincenc) (10.04.1850 - 26.01.1902) - чешский физик и гидродинамик. Исследовал колебания струн, процесс возникновение звука. Обнаружил, что причиной возникновения звука при колебании струны являются периодический отрыв воздуха и связанное с ним вихреобразование. Предложил критерий (число Струхаля), связывающий частоту колебаний потока со скоростью направленного течения и характерным размером [8].

РЕЙНОЛЬДС, ОСБОРН (Reynolds, Osborne) (23.08.1842-21.02.1912) - английский инженер и физик. Работы Рейнольдса посвящены механике, гидродинамике, теплоте, электричеству, магнетизму. В 1883 г. Рейнольдс установил, что ламинарное течение переходит в турбулентное, когда введенная им безразмерная величина (число Рейнольдса) превышает критическое значение. Число Рейнольдса широко используется при решении задач гидро- и аэродинамики в случае малых и средних дозвуковых скоростей. Рейнольдс определил механический эквивалент теплоты. Сконструировал ряд турбин и центробежных насосов [8].

Литература

1.  Бэтчелор Дж.  В кн.: Введение в динамику жидкости. М.: Мир, 1973. 760 с.
2. Беляев Е.Н., Черваков В.В. В кн. Математическое моделирование ЖРД. М.: МАИ, 2009. 278 с.
3. Ланда П.С. Срывной флаттер и эффект затягивания. Вестник научно-технического развития. № 6 (22), 2009. С. 10-19.
4. Хассан Ареф. Вихревая динамика волновых следов. Нелинейная динамика. т. 2, № 4, 2006. С. 411-424.
5. Вовк. И.В. Физический взгляд на природу эоловых тонов. Акустичний вiсник, т. 10, № 2. Киев, 2007. С. 22-32.
6. Мервин Е. Голдстейн. В кн. Аэроакустика. М.: Машиностроение,1981. 295 с.
7. Расходомер-счетчик вихревой газовый. Взлет ВРС. Санкт-Петербург, 2007. 26с.
8. Большая советская энциклопедия (3-е издание). М.: Советская энциклопедия, 1969-1978.
9. Бидерман В.Л. В кн. Теория механических колебаний. М.: Высшая школа, 1980. 408 с.