ТОЧНОЕ ПРОЕКТИРОВАНИЕ МОНО- И ДВУХСОСТАВНЫХ ЗАРЯДОВ РДТТ

Николай Юрьевич Кочетков, аспирант

 

Задача точного проектирования зарядов твердого топлива возникла одновременно с появлением стратегических и тактических ракет баллистического класса с РДТТ. С повышением защищенности наземных целей и снижением мощности боеголовок ракет требования к точности попадания в цель стали гораздо более жесткими. Обеспечение высокой точности доставки заряда к цели возможно только в случае, если расчетные и реальные давления в РДТТ совпадают.

В настоящее время точно проектируются только очень простые заряды, к которым относятся заряды с постоянной поверхностью горения в виде торцевидных конфигураций и телескопические с бронированными торцами. Все другие формы: зонтичные, канально-щелевые и прочие проектируются приближенно. В дальнейшем данные заряды длительно отрабатываются на экспериментальных моделях. В настоящее время отсутствуют точный способ проектирования моно- и, тем более, двухсоставных зарядов.

На базе нового метода расчета внутрибаллистических параметров был разработан метод точного проектирования моно- и двухсоставных зарядов и на его базе - программа МК-ГЕОМЕТРИЯ [1, 2]. Метод основан на принципе погашения дефицита поверхности горения на каждом шаге выгорания заряда. Существо метода заключается в следующем. Предполагается, что известен заряд-прототип, который приближенно выполняет условия ТЗ. Значения заданных в ТЗ давлений выполняются в среднем, причем в некоторых областях кривой Рк(t) они существенно превышают номинальные, а в некоторых недобирают. Пошаговый расчет, проведенный для реального времени по программе FILIKON, позволяет установить зависимости давления от времени и изменения площади поверхности горения по своду заряда. Для программы это одно и то же, так как существует однозначная связь:

S = A·F_кр·P_к^1-n и е = u·t,

где S - площадь поверхности горения заряда;
F_кр - площадь критического сечения сопла;
Р_к - давление в камере сгорания;
е, u, t - свод горения, скорость горения топлива и текущее время.

Величина коэффициента А в широком диапазоне величин давления остается постоянной. На каждом шаге эти зависимости корректируются. В расчетах эту коррекцию удобно проводить по зависимости S(е). При этом на каждом шаге по своду горения рассчитывается площадь поверхности заряда. Рассчитанное значение сравнивается с номинальным, соответствующим номинальному давлению в камере сгорания. При дефиците значения площади проводится операция погашения дефицита добавлением соответствующего значения. При профиците - производится изъятие части площади поверхности горения. Величина добавки-отбора площади реализуется в виде некоторой цилиндрической поверхности на каждом шаге. Добавка осуществляется пошагово с интервалом в величину единичного свода горения в направлении образующей. Количество шагов в направлении образующей влево и вправо фиксируется и приводится в соответствие с шагами в направлении горения заряда, то есть перпендикулярном образующей. Количество шагов в том и другом направлениях представляет собой параметрическую зависимость образующей, коррелированной с величиной поверхности заряда:

X = n·e;
Y = m·e.

Очевидно, что величина X является линейно зависимой от прироста-убыли вдоль цилиндрической поверхности горения.

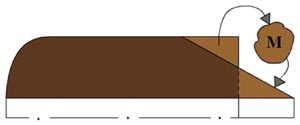
В случае, если имеется начальный цилиндрический участок поверхности горения заряда, величина его диаметра равна d₀. Если такого участка нет, то принимается любая точка на поверхности горения за условное начало отчета. Иллюстрирует принцип перераспределения массы заряда расчетная схема получения кривой Y(X).

Полученная зависимость Y(X) используется для "деформации" начального заряда путем пристыковки к нему дополнительной конфигурации. При этом образующие заряда переднего и заднего днищ являются криволинейными осями, относительно которых укладывается рассчитанная кривая корреляции. В случае, если кривая корреляции меняет знак относительно условной оси, то линия контура днища предполагает со стороны отрицательных значений отбор части заряда, а со стороны положительных - добавление.

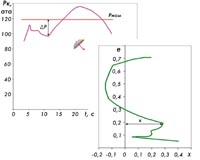
Поскольку величина добавки цилиндрической площади горения ΔS зависит линейно от длины ее образующей, то форма кривой Y(X) повторяет форму кривой ΔS(e). Натурные кривые давления, а, значит, и зависимости S(e), имеют достаточно сложный характер. Так, например, осциллограмма давлений в одном из двигателей первой ступени выглядит следующим образом. На начальном участке имеется крутой участок роста давления. В максимальной точке происходит излом и дальнейшее падение с переходом в область минимальных значений. После этого кривая плавно поднимается до максимального значения и после пологого максимума вновь начинает медленно понижаться. Такая же картина будет воспроизводиться и на корреляционной кривой. Сопоставление кривых изменения давления и корректирующей кривой говорит об их подобии. Этот факт стал ключевым при разработке инженерной методики коррекции заряда-прототипа с целью получения заряда, обеспечивающего постоянство давления. Действительно, если по одному известному из эксперимента значению давления определить величину отклонения 
P = P - P_ном и восстановить для этого момента времени величину дефицита площади  S = S - S_ном, затем найти длину образующей эквивалентного цилиндра X, то возможно определить постоянный коэффициент пересчета K_пер = X/ΔP. Далее все экспериментальные значения P(t) необходимо пересчитать в зависимость X(e), соответствующую корректирующей образующей заряда.

Для двухсоставного заряда в качестве прототипа используется доработанный монозаряд. Производится замена части высокотемпературного топлива вблизи сопла на низкотемпературное. Форма разделительной поверхности рассчитывается по методике, представленной в предыдущей статье [3].

Литература
1. Кочетков Н.Ю. Результаты разработки метода и программы расчета внутрибаллистических параметров РДТТ с двухсоставными зарядами. Материалы научно-технической конференции молодых ученых и специалистов им. Н.А. Кривошеева и В.В. Венгерского, Люберцы, 2008.
2. Кочетков Н.Ю. Разработка математического аппарата для расчета двухсоставных зарядов перспективных РДТТ двигательных установок космического назначения. Материалы XVIII научно-технической конференции молодых ученых и специалистов, Королев, 2008.
3. Кочетков Н.Ю. Математическое моделирование выгорания двухсоставных зарядов. Двигатель, № 4, 2008. С. 52-53.