МОДЕЛИ И АНАЛОГИИ МЕХАНИКИ ПЕРЕМЕЖАЕМЫХ И ПЕРЕМЕЖАЮЩИХСЯ СРЕД

"…И современник Галилея
Был Галилея не глупее
Он знал, что вертится Земля
Но… у него была семья…"
Евгений Евтушенко

Александр Григорьевич Прудников, д.т.н., ЦИАМ
Дмитрий Александрович Боев, вед. инженер, ЦИАМ

(Окончание. Начало в № 1 - 2008)

Во второй серии рисунков дана подборка опубликованных экспериментальных результатов "последнего двадцатисемилетия" по лобовым, боковым и кормовым искусственным пограничным течениям.

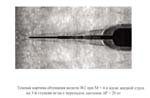
Основной результат решений, опытов и расчетов данных схем МПС: можно создать искусственные теплогазоаэродинамические обтекатели нулевого сопротивления трех вышеупомянутых видов с любым углом теплогазоаэродинамического отклонения набегающего воздушного потока, до 90^о включительно, но для наименьших потерь полного давления лучше до критического угла. Эксперименты разных стран это подтверждают.

В третьей группе рисунков приведена хронологическая подборка (из книг и статей 1960-1970 гг.) моделей МПС расчета параметров вихревых теплогазоаэродинамических процессов на примере простейших (естественных) пограничных течений: свободного, спутного плоского и осесимметричного погранслоя.

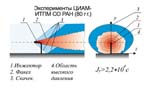
За рубежом последнее десятилетие "двухсредная" статистическая модель "диффузионного" волнового переноса, вихревого переноса, смешения и горения (монографии 62, 64, 71 гг.) известна как "Zimontmodel" (по фамилии В.Л. Зимонта, одного из "утекших" учеников московской школы горения). Основу "диффузионной модели" составляют: допущение однозначности односвязных поверхностей контактного и тангенциального разрыва; нормальное (гауссовское) распределение волнового и вихревого турбулентного переноса с определенной общей дисперсией.

Для спутных стабилизаторов пламени первая компонента, как уже отмечалось выше, равна нулю, а два других значения определялись неконтактным оптико-диффузионным методом. Полученные разными методами опытные зависимости дисперсий двух пассивных и реагирующих сред по длине и параметру спутности сразу же показали, что они одинаковы, отбросив, тем самым, все мифические теории "автотурбулентности" пламени. Логика вывода диффузионного дифференциального уравнения вероятностей переноса лагранжевых объемов любой субстанции, замыкающего систему уравнений движения, была свободна от известных ограничений градиентной аксиоматики Буссинеска, Рейнольдса, Прандтля и других авторов, последующих многочисленных "одно- и двухэтажных" моделей маттурбулентности, но она не определяла самого основного параметра: дисперсии субстанции (не говоря уже о параметрах горения) и плохо прикладывалась к пристеночным и многосредным пограничным течениям. К началу 70-х годов по структуре пограничных течений было накоплено достаточно много новых опытных фактов, чтобы начать разработку более общей вихревой модели МПС с ее главными составляющими; моделью мгновенного захвата (ММЗ) "телесной" птр скоростей первичным ядром крупного вихря: моделью вихревого клубка (МВК), с ее уравнениями движения для радиуса, поступательной, окружной скорости, теплогазодинамических параметров и формы вихря и аналитическими решениями; моделью постоянной завихренности (МПЗ) для кинетики вихря любого каскада и любого погранслоя и постоянной циркуляции МПЦ для любого надслоя спутных потоков, обтекающих независимо вихревой слой.

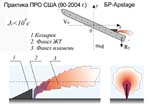
Аналитические решения МПС для таких профилей газодинамических параметров, как: профили температуры, продольной средней и пульсационной скорости спс и конфузорного ппс, построенные по МПЗ (с МПЦ и без нее) по-гауссовскому и максвелловскому распределению соответствующего масштаба, дают лучшие совпадения с опытом, чем известные "маттурбулентные" аппроксимации (для средних скоростей - это аппроксимации: Рейхардта, логарифмическая, степенная и т.п.; для пульсационных скоростей, совпадающих "маттурбулентных" аппроксимаций не существует).

Статистическая ("двухчленная") диффузионная модель, не учитывающая потенциальные компоненты скорости надслоя, также дает для спс хорошее совпадение с опытом. Известное эмпирическое число Прандтля для спс (D_v/D_T) = 0,5 (v, Т - индексы профиля скорости и температуры) также определяется аналитически из МПЗ.

В ограниченных рамках статьи опускаем другие, не менее интересные опытные наблюдения составляющих общей вихревой модели, показанные на стилизованных схемах физических экспериментов перехода птр в вихрь такие как: модель вторичного сдвига волны птр (реального явления, приводящего к уплотнению ядра вихря и появлению не нулевой вероятности паузы n даже в дорожке ядер вихрей Кармана; модели спаривания двух крупных вихрей или модели Перинга (МП) и др., для которых =2; модель "линейности в хаосе" (80-е годы) с ее системой дифференциальных уравнений для вероятности появления вихря i-го каскада, включая - вероятность встречи птр на длине погранслоя, определяющей функции: среднего масштаба вихря любого вихревого слоя и все его моменты в зависимости от длины погранслоя и параметра спутности, и замыкающей системы осредненных уравнений движения условного и общего осреднения (см. ранее в журнале "Двигатель" № 4, 2004).