ТУРБУЛЕНТНОСТЬ И СОЛИТОНЫ

Юрий Кочетков, начальник отделения
ФГУП "Исследовательский центр имени М.В. Келдыша", д.т.н.

Два уникальных явления были открыты почти одновременно. Но судьба их оказалась неодинаковой. Исследования, связанные с турбулентностью, продолжались непрерывно на протяжении следующих полутораста лет, а вот солитоны оказались практически забытыми и интерес к ним снова возник лишь относительно недавно. До сих пор ни одно из этих явлений не изучено до конца. Теории, описывающие указанные явления, не завершены. Будут ли они развиваться совместно? А может быть, это одно и то же?

Всего пятьдесят лет разделяют два замечательных гидродинамических наблюдения. В 1834 г. двадцатишестилетний шотландец Джон Скотт Рассел на протяжении двух миль мчался на лошади вдоль канала за оторвавшейся от баржи волной, которая не меняла своей формы и размеров. Впервые результаты своих наблюдений он документально зафиксировал в 1845 г., где назвал указанную волну "уединенной". А в 1883 г. английский профессор Осборн Рейнольдс описал свои знаменитые опыты с течением струек воды в прямоугольном канале. Он показал, что форма и взаимное положение подкрашенных струек зависят от размера канала, скорости и вязкости жидкости. При больших размерах и скоростях по мере убывания вязкости линии тока начинают колебаться относительно продольного направления, пересекаться (условно) и интенсивно перемешиваться. Так, почти одновременно, возникли два важных раздела физики, связанные с исследованиями так называемых солитонов и турбулентности.

В соответствии с гипотезой академика Ландау турбулентностью называют такой вид движения жидкости, когда с уменьшением вязкости постадийно увеличивается ее сложность. Это является следствием последовательных потерь устойчивости течениями менее сложной структуры. Другими словами, каждому режиму течения соответствует своя устойчивая область. И какой бы сложной эта область сегодня не казалась, преждевременно говорить о достижении изотропного хаоса. Постепенно, вследствие совершенствования экспериментального инструментария с большим разрешением и быстродействием, будут открываться новые, все более сложные виды устойчивости, последовательно выстраивающиеся в логическую цепочку. Важно подчеркнуть, что переходы из одного состояния устойчивости в другое дискретны. При этом со временем понятие турбулентного режима будет непрерывно изменяться, расширяя область так называемого переходного режима, а критическое число Рейнольдса будет постоянно увеличиваться.

Математическое описание перехода от ламинарного режима течения к турбулентному, основанное на линейной теории устойчивости, так и не обеспечило совпадения с практическими исследованиями, поскольку линеаризованные уравнения Навье-Стокса, кроме одномерного волнового уравнения, не имеют локализованных стационарных решений и не отражают волновых аспектов турбулентности. Турбулентность - одно из типичных волновых явлений природы. Полные уравнения Навье-Стокса являются нелинейными дифференциальными уравнениями второго порядка в частных производных, и поэтому они описывают волновые процессы, а их точные решения являются локализованными, стационарными или солитонными. Другими словами, солитонные решения - это решения, при которых выявляются особые устойчивые виды течений.

Согласно определению, приведенному в физической энциклопедии, солитон - локализованное стационарное или стационарное в среднем возмущение однородной или пространственно-периодической нелинейной среды. Основными свойствами солитонов являются их способность сохранять размеры, форму и скорость движения. При взаимодействии друг с другом их свойства не меняются.

Уникальное свойство солитонов сохранять размеры, форму и скорость эквивалентно сохранению импульса, энергии и момента количества движения, что происходит благодаря динамическому балансу между нелинейностью и дисперсией среды. При этом математическое понятие нелинейности среды, отражающее все физические особенности, приводящие к отличию от сред линейных, для которых характерны гармонические процессы, конкурирует с другим математическим понятием - дисперсией. Проявление нелинейности - это зависимость формы волны от ее амплитуды, вплоть до опрокидывания волны (прибой на берегу моря). Дисперсия в данном случае характеризует величину расплывания волны из-за различной скорости распространения волн разной длины. Нелинейность увеличивает скорость максимальной точки волны, а дисперсия замедляет ее движение.

Отсутствие одного из факторов приводит к тому, что солитон в данной ситуации не образуется. Очевидно, первое подтверждение взаимосвязи турбулентности с солитонами было продемонстрировано на примере уравнения Кортевега и де-Вриза для уединенной волны Дж. Ск. Рассела. Уравнение было получено из системы уравнений Навье-Стокса.
Второй член уравнения характеризует дисперсию, а третий - нелинейность среды.

В дальнейшем было показано, что многие природные турбулентные явления связаны с солитонами. Вихри и более сложные объекты, построенные из вихрей, являются многомерными солитонами. Солитон, образующийся на вихревой нити, называется спиральным солитоном. В более крупном масштабе спиральный солитон наблюдается в виде торнадо.

Ударные волны, впервые открытые Риманом в 1860 г., также являются солитонами. Приливная волна, заходящая из моря в устье, образует высокую водяную ступеньку, называемую бором. Бор - один из примеров ударной волны. Бор бежит быстрее, чем любая небольшая волна на поверхности воды. Увеличение крутизны фронта волны и ее опрокидывание превращает гигантский, но безвредный океанский солитон в страшное стихийное бедствие - цунами.

Если возвратиться к гипотезе Ландау, то можно сказать, что турбулентность есть цепочка солитонов, связанных между собой условиями устойчивости при все нарастающей интенсивности потока и снижающейся вязкости.

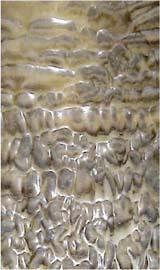
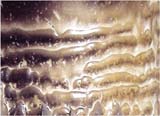
С помощью метода горячей визуализации (метода уноса массы, см. журнал "Двигатель", № 6 - 2004 г.) на модельных соплах из фторопласта были получены отпечатки турбулентного потока в виде устойчивых образований, а также зафиксированы области перехода из одного состояния в другое.

1. В области существенных положительных градиентов давления (dp/dx > 0) за вкладышем критического сечения сопла образуются парные винтовые течения с продольными осями вдоль стенки сопла. Это - вихри Тейлора-Гертлера. Их протяженность и диаметр среза зависят от крутизны контура. Возникают вихри в результате бифуркаций нормальных составляющих потока, попарно сворачивающихся и образующих вращающиеся компоненты винтового течения. Продольная компонента при этом примерно равна скорости невозмущенного потока.

2. При дальнейшем распрямлении контура сопла (dp/dx ~ 0) вихри Тейлора-Гертлера попарно скручиваются. Подобно тому, как пастух вьет из пучка конских волос наконечники своего кнута, течение из двух вращающихся навстречу газовых жгутов образует устойчивую скрутку. В результате в местах соприкосновения скруток друг с другом образуются локальные пары, вращающиеся в противоположных направлениях (спины), часть из которых выносит поток к стенке сопла, а часть от стенки. Та часть спинов, которая организует поток к стенке, формирует зоны растекания, другая - стекания. Спины расположены в шахматном порядке. Поэтому унос стенки имеет чередующуюся ячеистую структуру со сдвигом на полшага.

3. При медленном раскрытии сопла (dp/dx < 0) можно наблюдать эффект расплетания скруток. При этом ячеистая структура на стенке вырождается, образуя волнообразные борозды.

4. При значительном увеличении степени расширения сверхзвуковой части сопла жгуты упорядочиваются и укладываются в регулярную систему пересекающихся косых волн (волны Маха), которые проявляются на стенке в виде ромбовидных узоров.

5. При течении с отрицательным градиентом давления благодаря силам вязкого трения поток сборится и образуются волны Толмина-Шлихтинга. Вторичная потеря устойчивости приводит к режиму течения, аналогичному течению со скруткой потока (ячейки уноса расположены в шахматном порядке. Далее с раскрытием сопла возникают волны Маха.

Приведенные иллюстрации, полученные в результате экспериментов, могут быть приняты в качестве аргументов при изучении турбулентности на базе теории солитонов.