Отечественный и мировой опыт доводки и эксплуатации газотурбинных двигателей (ГТД) показывает, что появления случайных металлургических, технологических или эксплуатационных дефектов, приводящих к разрушению деталей, избежать невозможно. Полностью исключить возникновение трещин или учесть их наличие расчетными коэффициентами запаса не удается. В связи с этим одним из путей повышения безопасности ГТД, наряду с традиционными, должно быть обеспечение живучести, способности ответственных деталей сопротивляться развитию трещин.

В настоящей работе изложен расчетно-экспериментальный метод прогнозирования живучести ответственных деталей ГТД на примере их лопаток и дисков. Разрушение рассматривается как процесс развития трещины и описывается относительно простыми моделями линейной механики разрушения. Это позволяет сосредоточиться на учете специфики конструкции деталей, их нагружения, технологических и эксплуатационных факторов и получить представляющие практический интерес количественные характеристики живучести и надежности.

При прогнозировании живучести деталей двигателя необходимо решить комплекс взаимосвязанных задач, включающий анализ эксплуатационного нагружения детали и ее напряженного состояния, определение характеристик трещиностойкости материала и анализ процесса развития дефекта.

В соответствии с представлениями линейной механики разрушения поведение трещины при циклическом нагружении зависит от размаха коэффициента интенсивности напряжений (КИН). Для его расчета определяются напряжения, имеющие место в детали до появления трещины (номинальные напряжения). Поэтому первым этапом исследования живучести является детальный анализ номинального напряженного состояния. Он проводится с учетом изменения во времени режима и условий работы двигателя, статического и динамического нагружения детали и ее теплового состояния. В практике двигателестроения такой анализ выполняется на стадии конструирования независимо от задач обеспечения живучести и является обычным.

Для расчета коэффициентов интенсивности напряжений кроме номинальных напряжений необходимо знать положение, форму и размеры трещины. Эти данные могут быть получены при исследовании причин реальных поломок путем изучения изломов. При решении задач прогнозирования живучести необходимо рассчитывать КИН для достаточно полного набора возможных вариантов положения трещины и различных сочетаний ее размеров.

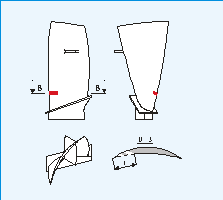
На лопатках вентилятора и компрессора наиболее вероятными местами появления трещин являются входная или выходная кромки профильной части, а также основание антивибрационной полки. Как показали расчеты и анализ изломов, в процессе роста трещина в лопатке сохраняет устойчивое соотношение основных размеров (устойчивую форму). Поэтому ее кинетика может быть описана одним параметром - размером со стороны корыта профиля. Скорость роста трещины в этом случае определяется средним по ее фронту значением КИН.

Зависимости КИН от размеров трещины для типичных случаев статического и динамического нагружения лопаток получены путем численного решения пространственной сингулярной задачи теории упругости методом конечных элементов. Среднее по фронту трещины значение КИН рассчитывается энергетическим методом. Расчеты проводятся для нескольких вариантов последовательного положения фронта трещины по мере ее роста, что позволяет получить зависимость КИН от длины трещины, в дальнейшем эта зависимость используется при расчете кинетики трещины.

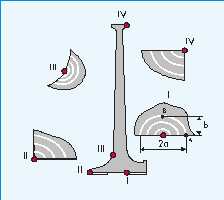
При моделировании разрушения дисков рассмотрены случаи инициализации трещин на внутренней поверхности, в переходе от ступицы к полотну, а также в угловых точках. Форма трещин на начальной стадии роста близка к дуге эллипса и описывается двумя параметрами - размерами полуосей. Кинетика трещины с криволинейным фронтом в рамках линейной механики разрушения определяется локальными коэффициентами интенсивности напряжений в характерных точках фронта. Для определения КИН в этом случае можно использовать известные соотношения для полуэллиптических и угловых трещин.

Основным соотношением математической модели процесса развития трещины является зависимость скорости роста трещины (СРТ) от коэффициента интенсивности напряжений. Известно несколько десятков эмпирических соотношений, описывающих экспериментальные данные по скорости роста трещин для различных материалов и условий нагружения. В настоящей работе использовано модифицированное уравнение Париса, описывающее весь диапазон скоростей роста трещин.

Принципиальным элементом описываемой методики является то, что характеристики трещиностойкости с целью наиболее полного учета металлургических и технологических факторов определяются на натурных деталях. Для этого разработана специальная методика проведения эксперимента и испытательный комплекс, позволяющий воспроизводить характерные для деталей ГТД условия развития трещин (нестационарный характер нагружения, взаимодействие квазистатических и динамических напряжений).

Важная особенность кинетики трещин в деталях ГТД заключается в том, что в реальных условиях эксплуатации параметры, определяющие поведение трещины, не являются детерминированными: имеют место отклонения режимов работы двигателя от типового полетного цикла, рассеяние размеров деталей, вариация свойств материала. Вследствие этого процесс развития трещин является случайным, а характеристики живучести лопаток - случайными величинами. Их расчет предваряется анализом закона распределения, что дает более полное представление о живучести. В описываемой методике для этого используется метод статистического моделирования.

Трещины деталей двигателя могут быть и неразвивающимися; в этом случае наработка до поломки не позволяет оценивать живучесть. В связи с этим предлагается ввести в качестве дополнительной характеристики живучести коэффициент запаса по циклической трещиностойкости.

Коэффициент запаса, как и долговечность, является величиной случайной и оценивается с помощью гистограммы распределения.

Статистическое моделирование позволяет непосредственно оценить вероятность поломки детали в течение заданного ресурса после появления макроскопической трещины.

Описанные математические модели реализованы в виде программного комплекса прогнозирования живучести деталей, включающего расчетные модули, базы данных о характеристиках материалов, нагрузках и условиях работы деталей, средства визуализации и удобный интерфейс.

Разработанную методику моделирования и реализующий ее программный комплекс можно использовать как инструмент при решении задач обеспечения живучести и безопасности двигателя на этапах проектирования, выбора материала и изготовления деталей, при обосновании выбора средств и периодичности диагностических осмотров, а также при анализе поломок, возникающих в процессе эксплуатации.

Рис.2. Схема лопатки вентилятора ГТД с трещиной на входной кромке	Рис.3. Типичные случаи возникновения трещин в диске компрессора ГТД