Владимир Скибин, Александр Крайко, Борис Блинник, Игорь Браилко, Михаил Иванов, Вячеслав Копченов, Владимир Макаров, Александр Секундов, Юрий Темис, ЦИАМ им. П.И. Баранова
Увеличение объема информации, необходимой для создания
новых объектов аэрокосмической техники, усложнение связей между элементами
проектируемых объектов и качественное изменение применяемого при этом математического
аппарата неминуемо приводит к тому, что важнейшим инструментом исследователя
и конструктора становится математическое моделирование (матмоделирование),
в основе которого лежат глубокое понимание происходящих в исследуемом объекте
физических и химических процессов, эффективные методы расчета и оптимизации
и стремительно развивающиеся средства вычислений, новые компьютерные и
информационные технологии. Авиационные двигатели на всех этапах своего
развития, будучи предельно энерго- и теплонапряженными и крайне сложными
в конструктивном отношении, должны были всегда удовлетворять строгим требованиям
по надежности, экономичности, ресурсу и весу, которые в настоящее время
резко ужесточились. Соответственно, возросли требования к качеству научного
сопровождения процесса создания авиадвигателей. Успешное развитие матмоделирования
в ЦИАМ как головном институте отрасли предопределили сформировавшиеся здесь
крупные научные школы Г.Г. Черного, Г.Н. Абрамовича и И.А. Биргера, которым
принадлежат многие выдающиеся научные достижения в области аэродинамики,
турбулентности и прочности.
Необходимость повышения достоверности описания сложных
газодинамических и физических процессов в авиационном двигателе и развитие
вычислительной техники привело к тому, что в начале 70-х гг. стали широко
применяться численные методы. В этот период в ЦИАМ впервые в практике газодинамических
расчетов стали широко использоваться для решения нестационарных задач монотонные
разностные схемы "распадного" типа. С их помощью были впервые решены смешанные
эллиптико-гиперболические задачи (например, прямая задача теории сопла
Лаваля). Почти одновременно в ЦИАМ была предложена подобная схема "маршевого"
счета двух- и трехмерных сверхзвуковых стационарных течений, не имевшая
конкурентов по эффективности и работоспособности. Расчеты, выполненные
с применением "распадных" схем, легли в основу вышедшей в 1976 г. под редакцией
родоначальника этого подхода С.К. Годунова монографии "Численное решение
многомерных задач газовой динамики". Эта монография, ставшая настольной
книгой нескольких поколений отечественных аэрогазодинамиков, обеспечила
заметный прогресс в двигателестроении. На Западе схемы такого типа (к которым
относятся, например, "TVD-схемы") получили широкое распространение примерно
с десятилетней задержкой. При активном участии ученых ЦИАМ численные методы
получили дальнейшее развитие. Так, для расчетов установившихся по времени
режимов в настоящее время обычно используются неявные схемы. Повышен порядок
аппроксимации и, что особенно важно, выполнено сохраняющее аппроксимацию
простое обобщение на произвольные нерегулярные разностные расчетные сетки.
"Распадные" схемы обеспечивают слабое размазывание ударных волн. Наряду
с этим, в расчетную практику вошло выделение главных разрывов в явном виде.
Для этих целей были созданы эффективные алгоритмы, позволившие с большей
достоверностью определять конфигурацию скачков уплотнения.
Первоначально схемы подобного типа применялись лишь при
интегрировании уравнений Эйлера, описывающих течения невязкого газа. Позже
они нашли применение и при интегрировании уравнений Навье-Стокса и Рейнольдса
для ламинарных и турбулентных течений и уравнений для неравновесных физико-химических
процессов. При матмоделировании наиболее важных в практике авиадвигателестроения
турбулентных режимов серьезной проблемой становится "замыкание" уравнений
Рейнольдса. Причина этого в том, что возможность учета вновь появляющейся
турбулентной вязкости не следует автоматически из основных принципов механики
сплошных сред, лежащей в основе традиционных методов расчетов. По этой
причине приходится вводить специальные уравнения, отражающие особенности
процессов сжимаемости, тепло-, массопереноса и обмена импульсов. Предложенные
существующей в ЦИАМ школой Г.Н. Абрамовича дифференциальные модели этих
процессов находятся на уровне лучших мировых аналогов.
ЦИАМ внес важный вклад в описание процесса горения. В
камере сгорания, где относительный уровень турбулентности достигает 50...100
%, смешение топлива с воздухом, а следовательно и горение практически полностью
определяется турбулентностью. В.Р. Кузнецов разработал теорию турбулентного
горения, в основе которой лежит физически обоснованное предположение о
тонкой зоне горения. Эта идея позволила математически строго разделить
область применимости уравнений газодинамики и уравнений кинетики. Благодаря
этому удается производить расчет трехмерного горения с учетом сотен реакций
между многими десятками химических компонент.
 |
 |
В качестве первого примера, демонстрирующего возможности
предложенных моделей турбулентности и тонкой зоны турбулентного горения,
приведем результаты расчета процессов в камере сгорания авиационного типа,
предназначенной для стационарной энергетической установки, работающей на
метане. Уравнения Рейнольдса замыкались предложенной в ЦИАМ однопараметрической
дифференциальной моделью турбулентности "*t-90". Главное внимание уделялось
выбросам окислов азота NOx. Учитывались все известные механизмы их образования:
механизм Зельдовича и "prompt". Установлено влияние перераспределения подвода
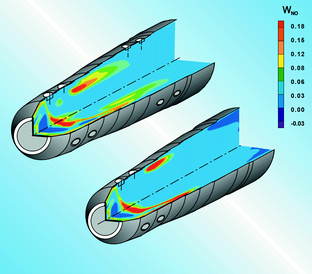
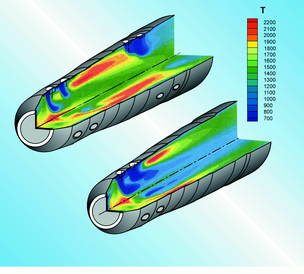
воздуха по длине камеры на образование окислов азота. На рис.1 и рис.2
приведены поля температур и скорости образования NOx для двух вариантов
конструкции камеры сгорания: первый - стандартный, второй - с увеличенным
подводом воздуха в головной части камеры через дополнительный ряд отверстий.
В результате такой модификации сократился объем высокотемпературных зон,
а выбросы NOx уменьшились на 30...40 %.
В качестве второго примера приведем результат расчета
обтекания турбинной лопатки высокотемпературным потоком с уровнем турбулентности
порядка 10 %. Поскольку совершенство турбины определяющим образом влияет
на эффективность двигателя, то учет турбулентности в набегающем потоке
приобретает особое значение. В этой связи укажем на особенности вязкого
течения у поверхности лопатки, где влияние турбулентности особенно заметно.
Это - тепловые потоки в переднюю кромку, струйное (пленочное) заградительное
охлаждение и переход от ламинарного режима к турбулентному (рис. 3). Во
всех трех случаях влияние уровня турбулентности Tu (Tu = u/U, где U - скорость
потока, а u - ее пульсация), ее масштаба L и числа Рейнольдса могут привести
к изменению тепловых потоков на лопатке по сравнению с бестурбулентным
обтеканием в 2..3 раза. Однако существующие модели турбулентности не предсказывают
такого эффекта, поскольку создавались для течений, в которых масштаб турбулентности
мал по сравнению с характерным размером задачи D (L/D << 1), в то
время как при обтекании турбинных лопаток отношение L/D существенно превышает
единицу.
 |
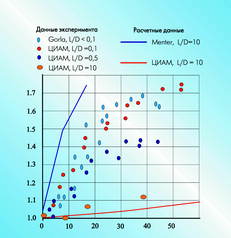 |
На рис.4 приведены экспериментальные и расчетные данные
для тепловых потоков в критической точке турбинной лопатки. Здесь Nu -
число Нуссельта, а Re - число Рейнольдса. По мере увеличения относительного
масштаба турбулентности L/D уровень тепловых потоков убывает. Между тем
наиболее точная модель Ментера из Центра им. Льюиса, хорошо работающая
в случае малых отношений L/D, с увеличением этой величины завышает экспериментальные
данные более чем на 50 %. Двухпараметрическая модель, предложенная в ЦИАМ
и совпадающая с американской при малом масштабе турбулентности, дает и
при большой его величине значения характеристик тепловых потоков, близкие
к наблюдаемым.
Сказанное не исчерпывает достижений ученых ЦИАМ в создании
базы матмоделирования применительно к проблемам авиадвигателестроения.
Так, применительно к задачам построения сопел разного типа были развиты
эффективные прямые и непрямые ("вариационные") методы оптимального профилирования.
Основанные на методе характеристик и на маршевых схемах сквозного счета
численные алгоритмы позволяют строить сопла, реализующие максимум тяги
при габаритных и иных дополнительных ограничениях, и определять их характеристики
на нерасчетных режимах.
(Продолжение в следующем номере)