НАУКА

(Окончание, начало см. в №№ 3, 4 и 5)

Матмоделирование особенно ценно в исследованиях, которые проводятся в связи с программами создания перспективных летательных аппаратов и силовых установок, а также других устройств, призванных обеспечить реализацию новых принципов и конструктивных схем и освоение, например, для воздушно-реактивных двигателей ранее недоступных скоростей полета. Такое положение обусловлено двумя причинами. Во-первых, экспериментальные исследования даже моделей таких объектов, требуют принципиально новых стендов, столь дорогостоящих, что решение об их создании нуждается в серьезном обосновании. Во-вторых, во многих случаях экспериментальные исследования на моделях бессмысленны из-за невозможности соблюдения необходимых критериев подобия.

Именно к таким объектам относятся прямоточные воздушно-реактивные двигатели, предназначенные для работы на гиперзвуковых летательных аппаратах (ГПВРД), и пульсирующие детонационные двигатели (ПДД). Для описания рабочего процесса и оптимизации (в интеграции с летательным аппаратом) силовых установок с ГПВРД и с ПДД разных типов в ЦИАМ разработаны математические модели и алгоритмы разного уровня. Ниже их возможности демонстрируются на примерах матмоделирования процессов в камере сгорания стационарного ГПВРД.

Камера сгорания ГПВРД является весьма сложным объектом матмоделирования. Горение в ней происходит в сверхзвуковом потоке смеси воздуха и топлива, например, водорода, подаваемого в камеру в виде отдельных сверхзвуковых струй. Процесс горения в значительной степени определяется смешением горючего и воздуха. Однако из-за сверхзвуковой скорости время пребывания горючего и окислителя в камере мало, в силу чего становится существенной конечная скорость химических реакций. Поэтому матмоделирование достаточно сложной ударно-волновой структуры потока многокомпонентной смеси в камере сгорания ГПВРД должно включать турбулентное перемешивание и неравновесные химические реакции.

Для расчета течений в тракте ГПВРД в ЦИАМ создан комплекс математических моделей и алгоритмов, основанных на решении параболизованных и полных уравнений Навье-Стокса и Рейнольдса. Учитываются пограничные слои на стенках. Уравнения Рейнольдса замыкаются дифференциальной моделью Vt-90. Для расчета сверхзвукового горения используются или модель бесконечно тонкого фронта пламени, или упрощенные и детальные схемы химической кинетики. Модификация модели тонкого фронта пламени, предложенной В.Р. Кузнецовым для дозвуковых течений, позволила учесть и при сверхзвуковом горении влияние турбулентных пульсаций. Численные методы основаны на модификациях схемы С.К. Годунова и ее стационарного аналога.

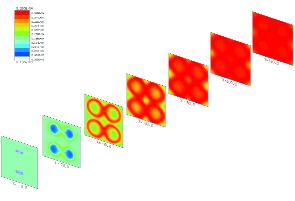
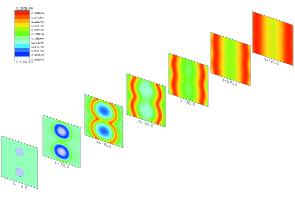
При больших числах Маха полета (Mп), когда поток в камере является преимущественно сверхзвуковым, интегрирование стационарных параболизованных уравнений Рейнольдса для двухмерных и пространственных течений ведется с помощью быстрых маршевых методов. При этом даже в трехмерном случае при расчетах на персональных компьютерах допускается использование детальных схем химической кинетики. Для режимов с большими гиперзвуковыми скоростями при спутной подаче топлива горение лимитируется смешением. Поэтому чрезвычайно важна его интенсификация, в чем существенна роль трехмерных эффектов. В качестве примера на рис. 1, а представлено поле температур, реализующееся при горении струй водорода в спутном сверхзвуковом потоке воздуха при подаче водорода через сверхзвуковые сопла с эллиптическими выходными сечениями. С удалением от среза сопла каждая струя водорода разделяется на две струи меньшего размера, что вызывает интенсификацию смешения. Для сравнения на рис. 1, б показано поле температур при подаче водорода через осесимметричные сопла. Эффект разделения струй подтвердили эксперименты, проведенные в ЦИАМ.

Рис. 1(а)	Рис. 1(б)

С уменьшением Mп в камере сгорания возникают сравнительно большие зоны дозвуковых скоростей. На таких режимах приходится решать полные, а не параболизованные уравнения Рейнольдса. В качестве примера такого расчета на рис. 2 представлены поля чисел Маха (а) и массовой концентрации воды (б) при горении струи водорода в круглой трубе в спутном сверхзвуковом потоке воздуха. Возникающие в потоке скачки, взаимодействуя с пограничным слоем, вызывают его отрыв с образованием обширной дозвуковой зоны.

Рис. 2(а)

Рис. 2(б)

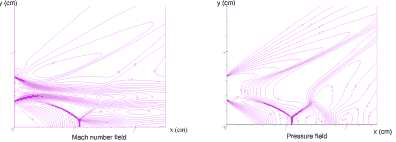
При сверхзвуковых скоростях в камере сгорания особого внимания требует матмоделирование воспламенения и стабилизации горения. Важность этой проблемы объясняется тем, что при малых временах пребывания в камере температура на входе может быть недостаточно высокой для самовоспламенения при приемлемых длинах. Предварительные оценки показывают, что это актуально для полета с Mп = 6...9. Здесь предлагаются специальные меры для обеспечения воспламенения и стабилизации горения, которые включают использование уступов, ниш, подачи топлива по нормали к стенке. Как и в предыдущем примере, моделирование этих ситуаций требует применения моделей, основанных на полных уравнениях Рейнольдса с детальной химической кинетикой. Возможности такого моделирования демонстрирует расчет выдува осесимметричной струи водорода в спутный сверхзвуковой поток воздуха через инжектор с кромкой конечной толщины. На рис. 3 показано поле температур в области, примыкающей к сечению подачи водорода. При работе воспламеняющего устройства (свечи) в области за донным торцом происходит воспламенение, которое сопровождается горением в основном потоке. Для иллюстрации картины течения в области, примыкающей непосредственно к кромке, на рис. 4 показаны поля чисел Маха и давления при отсутствии свечи.

Рис. 3	Рис. 4

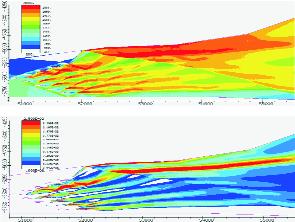
При расчете характеристик ГПВРД необходимо учитывать как интеграцию силовой установки и летательного аппарата, так и интеграцию элементов силовой установки (воздухозаборник - камера сгорания, камера сгорания - сопло). В качестве примера расчета, выполненного с учетом такой интеграции, на рис. 5 представлены поля массовой концентрации воды в камере сгорания ГПВРД при подаче водорода через систему пилонов. Расчет производился от носа летательного аппарата. Учитывалась неравномерность потока на входе в камеру. Решение получено в рамках параболизованных уравнений Рейнольдса. Показано, что для улучшения характеристик силовой установки необходимо раскрывать концевой участок камеры сгорания, чтобы повысить уровень рекомбинации продуктов сгорания.

Рис. 5

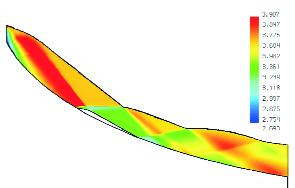
Методы матмоделирования позволяют оптимально профилировать авторегулируемые системы со сравнительно короткими центральными телами, заканчивающимися донным торцом. При заданных: высоте полета, условиях в камерах сгорания ЖРД, расстоянии между ними и максимально допустимой длине центрального тела такие конфигурации реализуют максимум тяги. Определение их тяги в нерасчетных условиях, в частности, при старте с Земли проводится с учетом отрыва пограничного слоя, который может возникать из-за взаимодействия с ним образующегося на таких режимах висячего скачка. На рис. 6 представлено поле чисел Маха в нерасчетной струе около оптимально спрофилированного контура центрального тела на старте с Земли. Видны висячий скачок и граница отрывной зоны. Благодаря развитому способу профилирования и авторегулируемости удается значительного уменьшить потери на старте сопел с центральным телом по сравнению с оптимальными в пустоте осесимметричными соплами той же степени расширения. В типичных случаях они уменьшаются в три-четыре раза (с 11 до 3 %).

Рис. 6

Как продемонстрировано на примерах моделирования течения в ГПВРД, методы матмоделирования позволяют прогнозировать возможности принципиально новых схем двигателей, силовых и энергетических установок и других устройств до создания "в железе" даже весьма отдаленных их модельных прототипов. К подобным объектам относится волновой ротор (wave rotor) - устройство, предназначенное для повышения максимальной температуры цикла тепловой машины при сохранении неизменной температуры продуктов сгорания перед турбиной, - самым теплонапряженным ее элементом.

Снижение температуры горячих продуктов сгорания в волновом роторе происходит благодаря тому, что до поступления на турбину они сжимают во вращающемся канале ротора холодный воздух, до этого поступивший в канал из компрессора. Воздух, сжатый продуктами сгорания, приходит в камеру сгорания, а охладившиеся продукты сгорания попадают на турбину. Передача энергии от горячих продуктов сгорания к воздуху происходит в нестационарном волновом процессе, который разыгрывается в каждом из десятков каналов ротора. Стенки каналов обтекаются попеременно горячим и холодным газами и поэтому остаются сравнительно холодными.

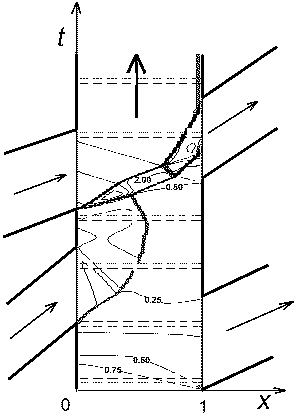
Для выяснения возможностей волнового ротора как потенциально перспективного устройства в ЦИАМ созданы математические модели, включающие расчет нестационарного течения газа в его каналах, выход на периодический для каждого канала режим течения, учет трения газа о стенки канала, вращения и конечности времени открытия и закрытия концов канала при их прохождении мимо подводящих и отводящих каналов (портов) и ряда других эффектов. К достоинствам одной из таких моделей относится явное выделение при счете на неподвижной сетке контактных разрывов, отделяющих воздух от продуктов сгорания. Возможности этой модели демонстрирует рис. 7. На нем для четырехпортового ротора показана развертка изолиний плотности, которую можно было бы наблюдать со стороны кожуха и верхней цилиндрической стенки всех каналов, будь они прозрачными. Кроме изолиний и их сгущений - контактных разрывов и скачков, на рисунке жирными линиями дана развертка боковых стенок кожуха и портов, а стрелками - направления потока в портах и направление вращения ротора. На изображенном периодическом для всех каналов режиме течения в среднем левые порты - входные, а правые - выходные, хотя в отдельные интервалы времени в них возможны допускаемые моделью обратные токи. Из нижнего левого порта воздух попадает в ротор компрессора, а из верхнего - продукты сгорания от камеры сгорания. Через верхний правый порт воздух и часть продуктов сгорания идут в камеру, а через нижний большая часть продуктов сгорания попадает на турбину.

Представленные примеры демонстрируют возрастающие возможности матмоделирования - эффективного инструмента исследователя и конструктора при создании сложнейших образцов техники, включая, авиационные двигатели ХХI века.