НАУКА

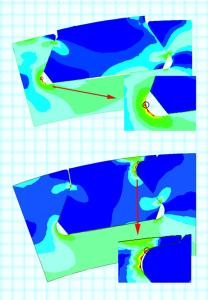
При параллельном проектировании лопатки и диска определяющим является замковое соединение. Его расчет предполагает многократное уточнение конструкций хвостовика и диска с лопатками по критерию обеспечения ресурса в зоне концентрации напряжений. Сказанное поясняет рис.1, на котором представлены результаты расчета этого узла, измененная форма его и поля напряжений в исходном (а) (сверху) и окончательном (б) (внизу) вариантах соединения. При отличии шкал напряжений на рис.1а и б кружки указывают наиболее опасные точки конструкции.

Рис.1	Рис. 2

Учет нелинейности совместного деформирования лопатки и диска важен для оценки зазоров между корпусом и лопаточным венцом и последующего уточнения газодинамического состояния компрессора. Нелинейные эффекты существенно сказываются на перемещениях и углах разворота периферийных сечений лопаток. Так, для высоконагруженной ступени вентилятора расчет по линейной модели дает углы разворота периферийного сечения в 2...3°, а расчет по нелинейной модели - менее 1°. Поэтому проектирование лопатки предполагает итерационный подход, связывающий газодинамический расчет течения, профилирование статический расчет лопатки и проектирование диска.

На основе описанных выше подходов созданы имитационные вычислительные стенды для моделирования изменения во времени течения охлаждающего воздуха через лабиринтные уплотнения и в полостях двигателя, теплового и НДС корпусов и роторов и размера зазоров в уплотнениях.

Применяемые методы позволяют рассчитывать течения и определять силовые характеристики сопел, поворот расширяющихся частей которых позволяет управлять направлением вектора тяги. Сопла такого типа, называемые обычно соплами с управлением вектором тяги (СУВТ) могут быть плоскими и осесимметричными. При повороте расширяющейся части течение в плоских соплах вдали от боковых стенок остается двумерным. При повороте расширяющейся части осесимметричного сопла течение в нем становится пространственным.

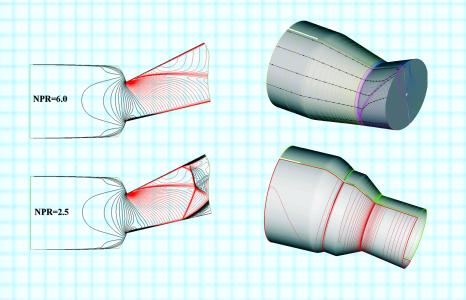
Основной газодинамической характеристикой обычного сопла является зависимость коэффициента тяги от перепада давления на сопле - NPR. Для СУВТ появляется еще одна важная характеристика, отражающая при фиксированном геометрическом угле поворота зависимость эффективного угла отклонения вектора тяги aeff от NPR. Характеристики сопел определялись в широком диапазоне значений NPR. Интегрирование уравнений Рейнольдса, замкнутых однопараметрической моделью турбулентности Vt-90, велось по неявной монотонной разностной схеме повышенного порядка аппроксимации.

Результаты численного моделирования течения в плоском СУВТ представлены на рис. 2а. Даны изолинии числа Маха для автомодельного режима работы (NPR = 6,0) и для одного нерасчетного режима с перерасширением потока (NPR = 2,5). Красные изолинии отвечают сверхзвуковым скоростям. Расчет подтвердил обнаруженные экспериментально экстремумы aeff при снижении NPR. Результаты расчета осесимметричных СУВТ (рис.2б) также согласуются с экспериментом. При больших углах отклонения течение в них является пространственным и в сверхзвуковой и в дозвуковой частях сопла. По этой причине здесь приходится решать трехмерную смешанную (до-, транс- и сверхзвуковую) прямую задачу теории сопла Лаваля. Расчеты в приближении уравнений Эйлера обнаружили сложный характер течения в сверхзвуковой части с перерасширением потока и с образованием ударных волн. Расчеты в рамках уравнений Рейнольдса подтвердили наличие таких отрывов.

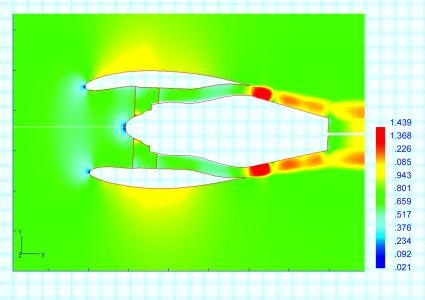
Методы матмоделирования позволят просчитать пространственное обтекание мотогондолы двухконтурного двигателя в интеграции с летательным аппаратом, а на режиме реверса с учетом влияния поверхности Земли. На рис. 3 представлены поля чисел Маха на внешних и внутренних поверхностях мотогондолы ТРДД сверхбольшой степени двухконтурности с биротативным вентилятором на крейсерском режиме полета с Mп = 0,75 и углом атаки a = 3°. Для наглядности представления в обечайке вентилятора сделан вырез, сквозь который можно видеть поля чисел Маха на обрамленных черными линиями активных и пассивном дисках, моделирующих венцы вентилятора и спрямляющем аппарате в хвостовой части мотогондолы, а также поле чисел Маха на входе в газогенератор.

Рис.3	Рис. 4

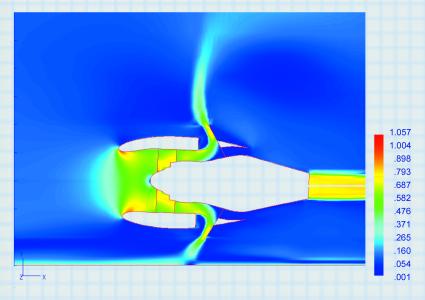
На рис. 4 в плоскости симметрии двигателя изображено поле чисел Маха в течении, возникающем при обтекании на крейсерском режиме полета мотогондолы ТРДД большой степени двухконтурности с однорядным вентилятором при Мп = 0,78, эффективных углах атаки a = 3,2° и скоса b = 1°. Видно, что на внешней стороне обечайки вентилятора нет заметных сверхзвуковых зон, в то время как на обечайке газогенератора формируется сверхзвуковая струя с ярко выраженной бочкообразной структурой. На режиме реверса поле чисел Маха в плоскости симметрии мотогондолы представлено на рис. 5.

Рис.5	Рис. 6

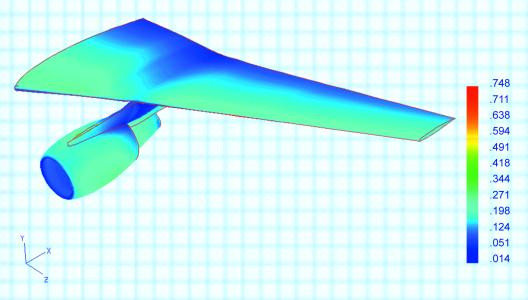
Расчеты такого типа даже при упрощенной геометрии реверсивного устройства позволяют оценить уровень обратной тяги, размер и форму струй, а также возможность их попадания на вход двигателя при разных скоростях внешнего потока. Как иллюстрация возможностей матмоделирования силовой установки, интегрированной с летательным аппаратом, на рис. 6 дано распределение чисел Маха на поверхностях крыла, пилона и мотогондолы того же двигателя при посадке самолета (Mп = 0,25, a = 8°, b = 0).

(Продолжение в следующем номере)